广东省广州市2018-2019学年高三上学期理数调研考试(零模)试卷
试卷更新日期:2019-02-12 类型:高考模拟
一、单选题
-
1. 设集合M= 则集合 =( )A、
 B、
B、 C、
C、 D、
D、 2. 若复数 是虚数单位)为纯虚数,则实数 的值为( )A、-2 B、-1 C、1 D、23. 已知 为等差数列,其前 项和为 ,若 , ,则公差 等于( ).A、1 B、 C、2 D、4. 若点 为圆 的弦 的中点,则弦 所在直线的方程为(A、
2. 若复数 是虚数单位)为纯虚数,则实数 的值为( )A、-2 B、-1 C、1 D、23. 已知 为等差数列,其前 项和为 ,若 , ,则公差 等于( ).A、1 B、 C、2 D、4. 若点 为圆 的弦 的中点,则弦 所在直线的方程为(A、 B、
B、 C、
C、 D、
D、 5. 已知实数 ,则 的大小关系是( )A、
5. 已知实数 ,则 的大小关系是( )A、 B、
B、 C、
C、 D、
D、 6. 下列命题中,真命题的是( )A、
6. 下列命题中,真命题的是( )A、 B、
B、 C、 的充要条件是
C、 的充要条件是  D、若
D、若  ,且
,且  ,则
,则  中至少有一个大于1
7. 由 的图象向左平移 个单位,再把图象上所有点横坐标伸长到原来的2倍得到 的图象,则 ( )A、
中至少有一个大于1
7. 由 的图象向左平移 个单位,再把图象上所有点横坐标伸长到原来的2倍得到 的图象,则 ( )A、 B、
B、 C、
C、 D、
D、 8. 已知甲袋中有1个黄球和2个红球,乙袋中有2个黄球和2个红球,现随机地从甲袋中取出两个球放入乙袋中,然后从乙袋中随机取出1个球,则从乙袋中取出红球的概率为( )A、 B、
8. 已知甲袋中有1个黄球和2个红球,乙袋中有2个黄球和2个红球,现随机地从甲袋中取出两个球放入乙袋中,然后从乙袋中随机取出1个球,则从乙袋中取出红球的概率为( )A、 B、 C、
D、
9. 已知抛物线 为双曲线 有相同的焦点F,点A是两曲线的一个交点,且AF⊥x轴,则双曲线的离心率为( )
C、
D、
9. 已知抛物线 为双曲线 有相同的焦点F,点A是两曲线的一个交点,且AF⊥x轴,则双曲线的离心率为( )
A、 B、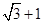 C、
C、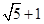 D、
D、 10. 已知等比数列 的前 项和为 ,若 ,则数列 的前 项和为( )A、
10. 已知等比数列 的前 项和为 ,若 ,则数列 的前 项和为( )A、 B、
B、 C、
C、 D、
D、 11. 如图为一个多面体的三视图,则该多面体的体积为( )
11. 如图为一个多面体的三视图,则该多面体的体积为( ) A、
A、 B、7
C、
B、7
C、 D、
D、 12. 已知过点 作曲线 的切线有且仅有两条,则实数 的取值范围是( )A、
12. 已知过点 作曲线 的切线有且仅有两条,则实数 的取值范围是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 已知实数 满足 ,则 的最小值为 .14. 已知向量 的夹角为45°,且 ,则 =15. 已知 ,则 .16. 在四面体 中, ,则该四面体体积的最大值为 .
三、解答题
-
17. 在△ABC中,角A、B、C所对的边分别为a、b、c,且 .(1)、求角C的大小;(2)、若A= ,△ABC的面积为 ,M为BC的中点,求AM.18. 某企业对设备进行升级改造,现从设备改造前后生产的大量产品中各抽取了100件产品作为样本,检测一项质量指标值,若该项指标值落在[20,40)内的产品视为合格品,否则为不合格品,图1是设备改造前样本的频率分布直方图,表1是设备改造后的频数分布表.

表1,设备改造后样本的频数分布表:
质量指标值
频数
2
18
48
14
16
2
(1)、请估计该企业在设备改造前的产品质量指标的平均数;(2)、企业将不合格品全部销毁后,并对合格品进行等级细分,质量指标值落在[25,30)内的定为一等品,每件售价240元,质量指标值落在[20,25)或[30,35)内的定为二等品,每件售价180元,其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率,现有一名顾客随机购买两件产品,设其支付的费用为X(单位:元),求X得分布列和数学期望.19. 如图,多面体ABCDEF中,四边形ABCD为矩形,二面角A-CD-F为60°,DE∥CF,CD⊥DE,AD=2,DE=DC=3,CF=6. (1)、求证:BF∥平面ADE;(2)、在线段CF上求一点G,使锐二面角B-EG-D的余弦值为 .20. 已知椭圆C: 的离心率为 ,点P 在C上.(1)、求椭圆C的方程;(2)、设 分别为椭圆C的左右焦点,过 的直线 与椭圆C交于不同的两点A、B,求△ 的内切圆的半径的最大值.
(1)、求证:BF∥平面ADE;(2)、在线段CF上求一点G,使锐二面角B-EG-D的余弦值为 .20. 已知椭圆C: 的离心率为 ,点P 在C上.(1)、求椭圆C的方程;(2)、设 分别为椭圆C的左右焦点,过 的直线 与椭圆C交于不同的两点A、B,求△ 的内切圆的半径的最大值.