甘肃省张掖市2018-2019学年高三上学期理数第一次联考试卷
试卷更新日期:2019-02-12 类型:高考模拟
一、单选题
-
1. 已知 , ,则 ( )A、
 B、
B、 C、
C、 D、
2. 已知复数 满足 ( 为虚数单位),则 的共轭复数所对应的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知 , ,则 ( )A、
D、
2. 已知复数 满足 ( 为虚数单位),则 的共轭复数所对应的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知 , ,则 ( )A、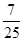 B、
B、 C、
C、 D、
D、 4. 如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )
4. 如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )
 A、2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件 B、2018年1~4月的业务量同比增长率均超过50%,在3月底最高 C、从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致 D、从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长5. 的内角 的对边分别为 ,若 ,且 ,则 的面积的最大值是( )A、 B、 C、 D、46. 已知单位向量 的夹角为 ,且 ,若向量 ,则 ( )A、9 B、10 C、3 D、
A、2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件 B、2018年1~4月的业务量同比增长率均超过50%,在3月底最高 C、从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致 D、从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长5. 的内角 的对边分别为 ,若 ,且 ,则 的面积的最大值是( )A、 B、 C、 D、46. 已知单位向量 的夹角为 ,且 ,若向量 ,则 ( )A、9 B、10 C、3 D、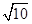 7. 为了得到 的图像,只需把函数 的图像( )A、向左平移
7. 为了得到 的图像,只需把函数 的图像( )A、向左平移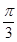 个单位长度
B、向右平移
个单位长度
B、向右平移 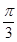 个单位长度
C、向左平移 个单位长度
D、向右平移 个单位长度
8. 已知抛物线 的焦点为 ,抛物线 的焦点为 ,点 在 上,且 ,则直线 的斜率为( )A、
个单位长度
C、向左平移 个单位长度
D、向右平移 个单位长度
8. 已知抛物线 的焦点为 ,抛物线 的焦点为 ,点 在 上,且 ,则直线 的斜率为( )A、 B、
B、 C、
C、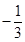 D、
D、 9. 如图, 是 上一点,分别以 为直径作半圆,从 作 ,与半圆相交于 , , ,在整个图形中随机取一点,则此点取自图中阴影部分的概率是( )
9. 如图, 是 上一点,分别以 为直径作半圆,从 作 ,与半圆相交于 , , ,在整个图形中随机取一点,则此点取自图中阴影部分的概率是( )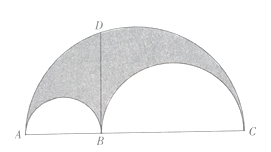 A、
A、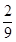 B、
C、
D、
10. 某几何体的三视图如图所示,则该几何体的各条棱中,最长的棱与最短的棱所在直线所成角的正切值为( )
B、
C、
D、
10. 某几何体的三视图如图所示,则该几何体的各条棱中,最长的棱与最短的棱所在直线所成角的正切值为( ) A、 B、 C、
A、 B、 C、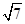 D、
11. 已知双曲线 的离心率为2, 分别是双曲线的左、右焦点,点 , ,点 为线段 上的动点,当 取得最小值和最大值时, 的面积分别为 ,则 ( )A、4 B、8 C、 D、412. 已知函数 ,若 ( ), , ,则 的取值范围是( )A、
D、
11. 已知双曲线 的离心率为2, 分别是双曲线的左、右焦点,点 , ,点 为线段 上的动点,当 取得最小值和最大值时, 的面积分别为 ,则 ( )A、4 B、8 C、 D、412. 已知函数 ,若 ( ), , ,则 的取值范围是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 在 的展开式中,含 的项的系数是 .14. 若 满足约束条件 ,则 的最小值为 .15. 已知 分别是定义在 上的奇函数和偶函数,且 ,当 时, ( 为常数),则 .16. 三棱锥 的每个顶点都在球 的表面上, 平面 , , , , ,则球 的表面积为 .
三、解答题
-
17. 已知等差数列 的公差 , 是数列 的前 项和, 是 和 的等比中项,且 是 和 的等比中项.(1)、求 的通项公式;(2)、若 ,求数列 的前 项和 .18. 某理财公司有两种理财产品 和 ,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品
投资结果
获利20%
获利10%
不赔不赚
亏损10%
概率
0.2
0.3
0.2
0.3
产品 (其中 )
投资结果
获利30%
不赔不赚
亏损20%
概率
0.1
(1)、已知甲、乙两人分别选择了产品 和产品 进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求 的取值范围;(2)、丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品 和产品 之中选其一,应选用哪种产品?19. 如图,在三棱锥 中, , , , , 分别为线段 上的点,且 , . (1)、证明: ;(2)、求二面角 的余弦值.20. 已知F为椭圆C: 的右焦点,点 在C上,且 .(1)、求椭圆C的方程;(2)、过F的直线 交C于A,B两点,交直线 于点M.判定直线PA,PM,PB的斜率是否依次构成等差数列?请说明理由.21. 已知函数 .(1)、若函数 在 上单调递减,求 的取值范围;(2)、若过点 可作曲线 的三条切线,证明: .
(1)、证明: ;(2)、求二面角 的余弦值.20. 已知F为椭圆C: 的右焦点,点 在C上,且 .(1)、求椭圆C的方程;(2)、过F的直线 交C于A,B两点,交直线 于点M.判定直线PA,PM,PB的斜率是否依次构成等差数列?请说明理由.21. 已知函数 .(1)、若函数 在 上单调递减,求 的取值范围;(2)、若过点 可作曲线 的三条切线,证明: .