湘教版九年级数学上册 4.3 解直角三角形 同步练习
试卷更新日期：2019-01-27 类型：同步测试
一、选择题
-
1. 在Rt△ABC中，∠C=90°，∠B=25°，AB=5，则BC的长为（ ）A、5sin25° B、5tan65° C、5cos25° D、5tan25°2. 如图，在△ABC中，∠A=30°，tanB= ，AC=2 ，则AB的长是（ ）
A、4 B、3+ C、5 D、2+23. 如图，在Rt△ABC中，∠C=90°，点B在CD上，且BD=BA=2AC，则tan∠DAC的值为（ ）
A、2+ B、2 C、3
D、3
4. 在△ABC中，AD是BC边上的高，∠C=45°，sinB= ，AD=1．则△ABC的面积为（ ）
A、1
B、
C、
D、2 
5. 如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD=1.5，BC=2，则cosB的值是（ ）
A、
B、
C、
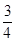D、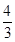
二、填空题
-
6. 已知△ABC中，AB=5，sinB= ，AC=4，则BC= ．7. 等腰△ABC的腰AC边上的高BD=3，且CD=5，则tan∠ABD= ．8. 如图，在网格中，小正方形的边长均为1，点A，B，C都在网格上，则∠ABC的正切值为 ．
9. 如图，点D在钝角△ABC的边BC上连接AD，∠B=45°，∠CAD=∠CDA，CA：CB=5：7，则∠BAD的余弦值为 ．
10. 如图，在△ABC中，AB=AC，sinA= ，BC=2 ，则△ABC的面积为 ．
三、解答题
