浙江省宁波市九校联考2017-2018学年高一上学期数学期末考试试卷
试卷更新日期:2019-01-25 类型:期末考试
一、单选题
-
1. 已知集合 , ,若 ,则 为( )A、
 B、
B、 C、
C、 D、
D、 2. 已知向量 , 满足| |=3,| |=2 ,且 ⊥( ),则 与 的夹角为( )A、 B、
2. 已知向量 , 满足| |=3,| |=2 ,且 ⊥( ),则 与 的夹角为( )A、 B、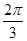 C、
C、 D、
3. 已知A是△ABC的内角且sinA+2cosA=-1,则tanA=( )A、
D、
3. 已知A是△ABC的内角且sinA+2cosA=-1,则tanA=( )A、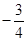 B、
B、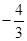 C、
D、
4. 若当 时,函数 始终满足 ,则函数 的图象大致为( )A、
C、
D、
4. 若当 时,函数 始终满足 ,则函数 的图象大致为( )A、 B、
B、 C、
C、 D、
D、 5. 将函数f(x)=sin(ωx+ )(ω>0)的图象向左平移 个单位,所得到的函数图象关于y轴对称,则函数f(x)的最小正周期不可能是( )A、
5. 将函数f(x)=sin(ωx+ )(ω>0)的图象向左平移 个单位,所得到的函数图象关于y轴对称,则函数f(x)的最小正周期不可能是( )A、 B、
B、 C、
C、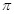 D、
D、 6. 已知f(x)= 是奇函数,则α,β的可能值为( )A、
6. 已知f(x)= 是奇函数,则α,β的可能值为( )A、 ,
,  B、
B、 ,
,  C、
C、 ,
,  D、
D、 ,
,  7. 设函数f(x)= ,则使得f(x)>f(2x-1)成立的x的取值范围是( )A、
7. 设函数f(x)= ,则使得f(x)>f(2x-1)成立的x的取值范围是( )A、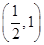 B、
B、 C、
C、 D、
D、 8. 已知| |=1,| |=2,∠AOB=60°, = + ,λ+2μ=2,则 在 上的投影( )A、既有最大值,又有最小值 B、有最大值,没有最小值 C、有最小值,没有最大值 D、既无最大值,双无最小值9. 在边长为1的正△ABC中, =x , =y ,x>0,y>0且x+y=1,则 • 的最大值为( )A、
8. 已知| |=1,| |=2,∠AOB=60°, = + ,λ+2μ=2,则 在 上的投影( )A、既有最大值,又有最小值 B、有最大值,没有最小值 C、有最小值,没有最大值 D、既无最大值,双无最小值9. 在边长为1的正△ABC中, =x , =y ,x>0,y>0且x+y=1,则 • 的最大值为( )A、 B、
B、 C、
C、 D、
D、 10. 定义在R上的偶函数f(x)满足f(x)=f(2-x),当x∈[0,1]时f(x)=x2 , 则函数g(x)=|sin(πx)|-f(x)在区间[-1,3]上的所有零点的和为( )A、6 B、7 C、8 D、10
10. 定义在R上的偶函数f(x)满足f(x)=f(2-x),当x∈[0,1]时f(x)=x2 , 则函数g(x)=|sin(πx)|-f(x)在区间[-1,3]上的所有零点的和为( )A、6 B、7 C、8 D、10二、填空题
-
11. 函数 的定义域为 .12. 计算: =;若2a=3b= ,a , b∈R , 则 + = .13. 已知 =(2,3), =(-1,k).若| =| |,则k=;若 , 的夹角为钝角,则k的范围为 .14. 已知函数f(x)=cos(2x ),则 =;若 ,x∈[- , ],
则sin(x )= .
15. 向量 与 的夹角为 ,若对任意的t∈R , | |的最小值为 ,则| |= .16. 已知函数f(x)= ,其中a>0且a≠1,若a= 时方程f(x)=b有两个不同的实根,则实数b的取值范围是;若f(x)的值域为[3,+∞],则实数a的取值范围是 .17. 若任意的实数a≤-1,恒有a•2b-b-3a≥0成立,则实数b的取值范围为 .三、解答题
-
18. 已知 =(cosx , sinx), =(1,0), =(4,4).
(Ⅰ)若 ,求tanx;
(Ⅱ)求| + |的最大值,并求出对应的x的值.
19. 已知函数f(x)=Asin(x+ ),若f(0)= .(Ⅰ)求A的值;
(Ⅱ)将函数f(x)的图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数g(x)的图象.
(i)写出g(x)的解析式和它的对称中心;
(ii)若α为锐角,求使得不等式g(α- )< )成立的α的取值范围.
20. 已知函数 ,角 的终边经过点 .若 是 的图象上任意两点,且当 时, 的最小值为 .(1)、求 或 的值;(2)、求函数 在 上的单调递减区间;(3)、当 时,不等式 恒成立,求 的最大值.
的最大值.