2016-2017学年福建省龙岩市上杭县九年级上学期期末数学试卷
试卷更新日期：2017-04-14 类型：期末考试
一、选择题
-
1. 下列图形中，是中心对称图形的是（ ）
A、
B、
C、
D、
2. 下列事件中，是不可能事件的是（ ）A、买一张电影票，座位号是奇数 B、射击运动员射击一次，命中9环 C、明天会下雨 D、度量三角形的内角和，结果是360°3. 方程x2=2x的根是（ ）A、0 B、2 C、0或2 D、无解4. 已知反比例函数y=﹣ ，则下列各点在此函数图象上的是（ ）A、（2，4） B、（﹣1，﹣8） C、（﹣2，﹣4） D、（4，﹣2）5. 将二次函数y=x2的图象向左平移1个单位，则平移后的二次函数的解析式为（ ）A、y=x2﹣1 B、y=x2+1 C、y=（x﹣1）2 D、y=（x+1）26. 有一个正方体，6个面上分别标有1～6这6个整数，投掷这个正方体一次，则出现向上一面的数字为偶数的概率是（ ）A、 B、 C、 D、7. 在平面直角坐标系中，⊙P的圆心坐标为（4，8），半径为5，那么x轴与⊙P的位置关系是（ ）A、相交 B、相离 C、相切 D、以上都不是8. 如图，线段AB是⊙O的直径，弦CD丄AB，∠CAB=20°，则∠AOD等于（ ）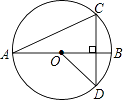
A、160° B、150° C、140° D、120°9. 若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，则k的取值范围是（ ）A、k＞1 B、k＞﹣1且k≠0 C、k≥﹣1且k≠0 D、k＜1且k≠010. 某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映，如果调整商品售价，每降价1元，每星期可多卖出20件．设每件商品降价x元后，每星期售出商品的总销售额为y元，则y与x的关系式为（ ）A、y=60（300+20x） B、y=（60﹣x）（300+20x） C、y=300（60﹣20x） D、y=（60﹣x）（300﹣20x）二、填空题
-
11. 在半径为6的⊙O中，120°的圆心角所对的弧长是 ．12. 请写一个图象在第二、四象限的反比例函数解析式： ．13. 已知方程x2+mx+3=0的一个根是1，则它的另一个根是 ．14. 反比例函数y= 的图象经过A（x1 ， y1），B（x2 ， y2）两点，其中x1＜0＜x2且y1＞y2 ， 则k的范围是 ．15. 如图，在△ACB中，∠BAC=50°，AC=4，AB=6．现将△ACB绕点A逆时针旋转50°得到△AC1B1则阴影部分的面积为 ．
16.已知，正六边形ABCDEF在直角坐标系的位置如图所示，A（﹣1，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°经过5次翻转之后，点B的坐标是 ．
三、解答题
-
17. 解方程：(1)、4x2﹣9=0(2)、x（2x﹣5）=4x﹣10．18.
如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（3，﹣1）．以原点O为对称中心，画出△ABC关于原点O对称的△A′B′C′，并写出A′、B′、C′的坐标．
19. 某地区2014年投入教育经费2500万元，2016年投入教育经费3025万元，求2014年至2016年该地区投入教育经费的年平均增长率．20. 如图，正三角形ABC内接于⊙O，若AB= cm，求⊙O的半径．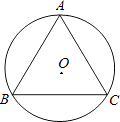
21. 如图，点P是正方形ABCD内一点，点P到点A、B和D的距离分别为1，2 ， ，△ADP沿点A旋转至△ABP′，连结PP′，并延长AP与BC相交于点Q．
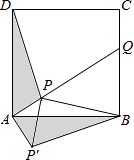(1)、求证：△APP′是等腰直角三角形；(2)、求∠BPQ的大小．22. 将分别标有数字1，2，3的三张卡片洗匀后，背面朝上放在桌面上．(1)、随机地抽取一张，求P（奇数）；(2)、随机地抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，求组成的两位数是4的倍数的概率．23. 如图，一次函数y=kx+b与反比例函数y= 的图象交于A（2，3），B（﹣3，n）两点．
(1)、求反比例函数的解析式；(2)、过B点作BC⊥x轴，垂足为C，若P是反比例函数图象上的一点，连接PC，PB，求当△PCB的面积等于5时点P的坐标．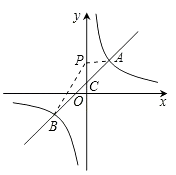
24. 如图，AB是⊙O的直径，点P是弦AC上一动点（不与A，C重合），过点P作PD⊥AB，垂足为D，射线DP交 于点E，交过点C的切线于点F．
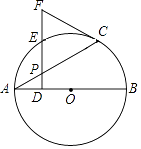(1)、求证：FC=FP；(2)、若∠CAB=30°，当E是 的中点时，判断以A，O，C，E为顶点的四边形是什么特殊四边形，并说明理由．25.如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A，B两点，与y轴交于点C（0，﹣3），A点的坐标为（﹣1，0）．
(1)、求二次函数的解析式；(2)、若点P是抛物线在第四象限上的一个动点，当四边形ABPC的面积最大时，求点P的坐标，并求出四边形ABPC的最大面积；
(3)、若Q为抛物线对称轴上一动点，直接写出使△QBC为直角三角形的点Q的坐标．