湖北省襄阳市襄城区2017-2018学年七年级上学期数学期中考试试卷

试卷更新日期：2019-01-24 类型：期中考试

进入出卷网下载

一、单选题

1. ﹣2的相反数是（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、 ﹣ $\frac{1}{2}$

查看试题解析
2. 下列运算正确的是（）

A、3a+2a=5a² B、3a+4b=7ab C、a⁵-a²=a³ D、2a²b-a²b=a²b

查看试题解析
3. 一种面粉的质量标识为“25±0.25千克”，则下列面粉中合格的是（）

A、24.70千克 B、25.30千克 C、24.80千克 D、25.51千克

查看试题解析
4. 在式子 $\frac{1}{x}$ ，2x+5y，0.9，﹣2a，﹣3x²y， $\frac{x + 1}{3}$ 中，单项式的个数是（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
5. 如果两个数的和是负数,那么这两个数（）

A、至少有一个为正数 B、同是正数 C、同是负数 D、至少有一个为负数

查看试题解析
6. 多项式 $\frac{1}{2}$ x^|m|−(m−4)x+7是关于x的四次三项式，则m的值是（）

A、4 B、-2 C、-4 D、4或-4

查看试题解析
7. 一个有理数和它的相反数之积一定为（）

A、正数 B、非正数 C、负数 D、非负数

查看试题解析
8. 一个多项式与x²﹣2x+1的和是3x﹣2，则这个多项式为（）

A、x²﹣5x+3 B、﹣x²+x﹣1 C、﹣x²+5x﹣3 D、x²﹣5x﹣13

查看试题解析
9. 计算2⁴+2⁴+2⁴+2⁴的结果是（）

A、2¹⁶ B、8⁴ C、2⁸ D、2⁶

查看试题解析
10. 有理数a，b在数轴上的位置如下图所示，在下列结论中：①ab＜0；②a+b＞0；③a³＞b²；④（a-b）³＜0；⑤a＜-b＜b＜-a；⑥|b-a|-|a|=b.正确的结论有（）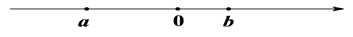

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

11. 地球上海洋面积约为36100万km² ，可用科学记数法表示为km² ．

查看试题解析
12. 已知|x|=|y|，x=-3，则y=.

查看试题解析
13. 在(-1)³ ， (-1)² ， -2² ， (-2)³这四个数中,最大的数与最小的数的和等于.

查看试题解析
14. 如果 $\frac{1}{5} a^{2} b^{3}$ 与 $- \frac{1}{4} a^{x + 1} b^{x + y}$ 是同类项，那么xy=.

查看试题解析
15. 多项式x²-3mxy-6y²+12xy-9合并后不含xy项,则m=.

查看试题解析
16. 已知:a，b互为相反数,c与d互为倒数,|m|=2，则 $\frac{a + b}{m} - c d + m^{3}$ =.

查看试题解析

三、解答题

17. 计算：

(1)、 $- 3^{2} + | - 5 | - {(- \frac{2}{3})}^{2} \times | 7 - (- 11) | + (- \frac{1}{3})$

(2)、 $(- \frac{1}{6}) \div (- \frac{1}{2} - \frac{1}{3}) + {(- 2)}^{2} \times (- 14)$

(3)、 $(- 49 \frac{6}{7}) \times (- 7)$

(4)、 $| - 10 | + [{(- 4)}^{2} - (1 - 3^{2}) \times 2]$

查看试题解析
18. 化简求值: $12 (x^{2} y - \frac{1}{3} x y^{2}) + 5 (x y^{2} - x^{2} y) - 2 x^{2} y$ ,其中 $x = \frac{1}{5}, y = - 5$ .

查看试题解析
19.

(1)、 $- [2 m - 3 (m - n + 1) - 2] - 1$

(2)、 $5 x^{2} - 2 (3 y^{2} - 5 x^{2}) + (- 4 y^{2} + 7 x y)$

查看试题解析
20. 已知:多项式 2x²+my-12与多项式nx²-3y+6的差与x，y的大小无关.
求:m+n+mn的值.

查看试题解析
21. 如图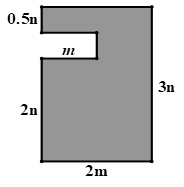

(1)、各线段长度如图标记，请用含 $m ， n$ 的式子表示阴影部分的面积；

(2)、若(1)中的 $m ， n$ 满足 $| m - 3 | + {(n - 2)}^{2} = 0$ ，请计算阴影部分的面积.

查看试题解析
22. 设一个两位数的个位数字为a，十位数字为b（a，b均为正整数，且a＞b），若把这个两位数的个位数字和十位数字交换位置得到一个新的两位数，则新的两位数与原两位数的差一定是9的倍数，试说明理由．

查看试题解析
23. 某出租车司机国庆节的营运全是在长虹路南北方向上进行的,如果规定向北为正,向南为负,他这天行车里程(单位:千米)如下: $- 10, + 5, - 2.4, + 4.4, + 15, + 5, - 16, + 12$

(1)、最后一名乘客送到目的地时,出租车在出发点的哪个方向?与出发点的距离?

(2)、长虹路南北至少有多少千米?

(3)、若该出租车耗油量为每千米0.08升,每升油7.5元,出租车按物价部门规定,起步价(不超过3千米)5元,超过3千米的部分,每千米(不足1千米按1千米计算)加价2元,该出租车司机今天的纯收入为多少元?（纯收入=收入－油耗钱）

查看试题解析
24. 如图，在数轴上每相邻两点之间的距离为一个单位长度.

(1)、若点A，B，C，D对应的数分别是a，b，c，d，则可用含 $a$ 的整式表示d为，若3d-2a=14，则b= c=(填具体数值)

(2)、在(1)的条件下，点A以4个单位/秒的速度沿着数轴的正方向运动，同时点B以2个单位/秒的速度沿着数轴的正方向运动，当点A到达D点处立刻返回，与点B在数轴的
某点处相遇，求相遇点所对应的数.

(3)、如果点A以2个单位/秒的速度沿着数轴的负方向运动，同时点B以4个单位/秒的
速度沿着数轴的正方向运动，是否存在某时刻使得点A与点B 到点C的距离相等，若存在请求出时间t，若不存在请说明理由.

查看试题解析