湖北省宜昌市东部2018届九年级上学期数学期中考试试卷
试卷更新日期：2019-01-24 类型：期中考试
一、单选题
-
1. 下列方程中，是一元二次方程的是（ ）A、
B、
C、
D、
2. 下列既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
3. 用配方法解一元二次方程 时，方程变形正确的是（ ）A、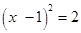
B、
C、
D、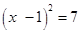
4. 若关于 的一元二次方程 有两个不相等的实数根，则 的取值范围是（ ）A、 B、
C、
D、
5. 已知点P(－1，m2＋1)与点Q关于原点对称，则点Q一定在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 抛物线y＝2(x－1)2－3的顶点、对称轴分别是（ ）A、(－1，－3)，x＝－1 B、(1，－3)， x＝－1 C、(1，－3)， x＝1 D、(－1，－3)，x＝17. 将抛物线y＝－2x2＋1向右平移1个单位，再向上平移2个单位后所得到的抛物线为（ ）A、y＝－2(x＋1)2－1 B、y＝－2(x＋1)2＋3 C、y＝－2(x－1)2＋1 D、y＝－2(x－1)2＋38. 到△ABC的三个顶点距离相等的点是△ABC的（ ）A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三边中垂线的交点9. 若α、β是方程x2+2x-2017=0的两个实数根，则α2+3α+β的值为（ ）A、2017 B、0 C、2015 D、201910. 一次函数y=ax+c（a≠0）与二次函数 （a≠0）在同一平面直角坐标系中的图象可能是（ ）A、
B、
C、
D、
11. 若二次函数y=ax2+bx+c（a＜0）的图象如图所示，且关于x的方程ax2+bx+c=k有两个不相等的实根，则常数k的取值范围是（ ）
A、0＜k＜4 B、-3＜k＜1 C、k＜-3或k＞1 D、k＜412. 改革的春风吹遍了神州大地，人们的生活水平显著的提高，国内生产总值迅速提高，2000年国内生产总值（GDP）约为8.75万亿元，计划到2020年国内生产总值比2000年翻两番，设以十年为单位计算，设我国每十年国内生产总值的增长率为x，则可列方程（ ）A、
B、
C、
D、
13. 如图，图案均是用长度相等的小木棒，按一定规律拼搭而成，第一个图案需4根小木棒，则第6个图案小木棒根数是（ ）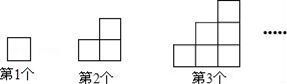
A、54 B、63 C、74 D、84二、解答题
-
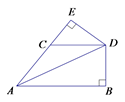
14. 解方程(1)、x2＋x－12＝0(2)、2x2-3x+2=015. 如图，在等腰△ACD中，AC=CD，且CD∥AB，DE⊥AC，交AC延长线于点E，DB⊥AB于B。
求证：DE=DB.
16. 某校九年级6个班的学生在矩形操场上举行新年联谊活动，学校划分6个全等的矩形场地分给班级，相邻班级之间留4米宽的过道（如图所示），已知操场的长是宽的2倍，6个班级所占场地面积的总和是操场面积的 ，求学校操场的宽为多少米？
17. 如图，需在一面墙上绘制几个相同的抛物线型图案．按照图中的直角坐标系，最左边的抛物线可以用y＝ax2＋bx(a≠0)表示．已知抛物线上B，C两点到地面的距离均为 m，到墙边OA的距离分别为 m， m.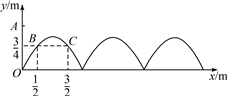
(1)、求该拋物线的函数关系式，并求图案最高点到地面的距离；(2)、若该墙的长度为10 m，则最多可以连续绘制几个这样的拋物线型图案？18. 已知一元二次方程x2﹣（2k+1）x+k2+k=0．(1)、求证：方程有两个不相等的实数根；(2)、若△ABC的两边AB、AC的长是这个方程的两个实数根，第三边BC的长为5．当△ABC是等腰三角形时，求k的值．19. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，三个顶点的坐标分别为A（2，2），B（1，0），C（3，1）．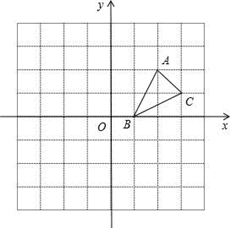
①将△ABC关于x轴作轴对称变换得△A1B1C1 ， 则点C1的坐标为；
②将△ABC绕原点O按逆时针方向旋转90°得△A2B2C2 ， 则点C2的坐标为；
③△A1B1C1与△A2B2C2成中心对称吗？若成中心对称，则对称中心的坐标为 ．
20. 【阅读理解】某科技公司生产一种电子产品，该产品总成本包括技术成本、制造成本、销售成本三部分。经核算，2016年该产品各部分成本所占比例约为2：a：1，且2016年该产品的技术成本、制造成本分别为400万元、1400万元。
(1)、确定a的值，并求2016年产品总成本为多少万元。(2)、为降低总成本，该公司2017年及2018年增加了技术投入，确保这两年技术成本都比前一年增加一个相同的百分数m(m<50%)，制造成本在这两年里都比前一年减少一个相同的百分数2m；同时为了扩大销售量，2018年的销售成本将在2016年的基础上提高10%，经过以上变革，预计2018年该产品总成本达到2016年该产品总成本的 。求m的值。21. 如图（1），在Rt△ABC中，∠A=90°，AC=AB=4，D，E分别是AB，AC的中点．若等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1 ， 如图（2），设旋转角为α（0＜α≤180°），记直线BD1与CE1的交点为P．
(1)、求证：BD1=CE1；(2)、当∠CPD1=2∠CAD1时，求CE1的长；(3)、连接PA，△PAB面积的最大值为 ． （直接填写结果）22. 抛物线 和直线 （k为正常数）交于点A和点B，其中点A的坐标是（-2，1），过点A作x轴的平行线交抛物线于点E，点D是抛物线上B、E之间的一个动点，设其横坐标为t，经过点D作两坐标轴的平行线分别交直线AB于点C、M，设CD=r，MD=m。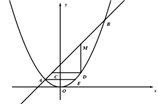
(1)、根据题意可求出a= ， 点E的坐标是。(2)、当点D可与B、E重合时，若k=0.5，求t的取值范围，并确定t为何值时，r的值最大。(3)、当点D不与B、E重合时，若点D运动过程中可以得到r的最大值，求k的取值范围，并判断当r为最大值时m的值是否最大，说明理由。