湖北省孝感市云梦县2018届九年级上学期数学期中考试试卷

试卷更新日期：2019-01-24 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形（     ）
    A、 B、   C、 D、

    查看试题解析

  • 2. 若抛物线y=（x﹣m）2+（m﹣1）的顶点在第一象限，则m的取值范围为（   ）
    A、m＞0 B、m＞1 C、m＞﹣1 D、0＜m＜1

    查看试题解析

  • 3. 在某次同学聚会上，每两个人都握一次手，所有人共握手45次，设有x人参加这次聚会，则列出方程正确的是（   ）
    A、x（x+1）=45 B、x（x﹣1）=45 C、 =45 D、 =45

    查看试题解析

  • 4. 已知x=2是一元二次方程（m﹣2）x2+4x﹣m2=0的一个根，则m的值为（　　）


    A、2 B、0或2 C、0或4 D、0

    查看试题解析

  • 5. 已知点A（a，1）与点A′（4，b）关于原点对称，则a、b的值分别为（   ）
    A、a=﹣4，b=﹣1 B、a=﹣1，b=﹣4 C、a=1，b=4 D、a=4，b=1

    查看试题解析

  • 6. 若方程ax2+bx+c=0的两个根是﹣4和2，那么二次函数y=ax2+bx+c的图象的对称轴是直线（   ）
    A、x=﹣2 B、x=﹣1 C、x=0 D、x=1

    查看试题解析

  • 7. 如图，是一个横断面为抛物线形状的拱桥，当水面宽4m时，拱顶（拱桥洞的最高点）离水面2m，当水面上升1m时，水面的宽为（   ）

    A、 2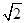 m B、2m C、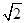 m D、3m

    查看试题解析

  • 8. 如图，⊙C过原点O，且与两坐标轴分别交于点A、B，点A的坐标为（0，2），M是第三象限内⊙C上一点，∠BMO=120°，则圆心C的坐标为（   ）

    A、（1，1） B、 （1， 3 ） C、（2，1） D、 （﹣ 3 ，1）

    查看试题解析

  • 9. 已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是x=1，下列结论：①abc＜0；②b2＞4ac；③a+b+c＜0；④3a+c＞0，其中正确结论的个数为（   ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题

  • 10. 若x=0是一元二次方程x2+2x+a=0的一根，则另一根为 ．

    查看试题解析

  • 11. 抛物线y=x2﹣2x+2与坐标轴交点个数为个．

    查看试题解析

  • 12. 将△ABC绕着点C顺时针方向旋转60°后得到△A′B′C′，若∠A=50°，∠B′=100°，则∠BCA′的度数是 ．

    查看试题解析

  • 13. 若实数x满足x2﹣2x﹣1=0，则2x3﹣7x2+4x﹣2017= ．

    查看试题解析

  • 14. 如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，B为AN弧的中点，P是直径MN上一动点，则PA+PB的最小值为 ．

    查看试题解析

  • 15. 如图，点B的坐标是（0，1），AB⊥y轴，垂足为B，点A在直线y= 33 x，将△ABO绕点A顺时针旋转到△AB1O1的位置，使点B的对应点B1落在直线y= 33 x上，再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置，使点O1的对应点O2落在直线y= 33 x上，依次进行下去…，则点O100的纵坐标是 ．

    查看试题解析

三、解答题

  • 16. 用指定的方法解下列方程：
    (1)、2x2﹣4x+1=0（公式法）
    (2)、2x2+5x﹣3=0（配方法）

    查看试题解析

  • 17. 如图，分别画出△ABC绕点O逆时针旋转90°和180°后的图形．

    查看试题解析

  • 18. 如图，二次函数y=ax2+bx+c（a≠0）的图象的顶点C的坐标为（﹣1，﹣3），与x轴交于A（﹣3，0）、B（1，0），根据图象回答下列问题：

    (1)、写出方程ax2+bx+c=0的根；
    (2)、写出不等式ax2+bx+c＞0的解集；
    (3)、若方程ax2+bx+c=k有实数根，写出实数k的取值范围．

    查看试题解析

  • 19. 已知关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1 ， x2 ．
    (1)、求m的取值范围；
    (2)、若x1 ， x2满足2x1=|x2|+3，求m的值．

    查看试题解析

  • 20. 如图，AB是⊙O的直径，弦CD⊥AB于点E，点F在⊙O上，FD恰好经过圆心O，连接FB．

    (1)、若∠F=∠D，求∠F的度数；
    (2)、若CD=24，BE=8，求⊙O的半径．

    查看试题解析

  • 21. 某城市中心地带有一楼盘，开发商准备以每平方7000元的价格出售，由于国家出台了有关调控房地产的政策，开发商决定下调售价，有两种方案：

    方案一：经过连续两次下调售价，以每平方米5670元的价格销售；

    方案二：先下调5%，再下调15%；

    (1)、求方案一中平均每次下调的百分率；
    (2)、请问哪种方案对购房者更优惠？为什么？

    查看试题解析

  • 22. 如图，△ABC中，∠ACB=90°，AC=BC=2，将△ABC绕点C逆时针旋转得到△A1B1C，旋转角α（0°＜α＜90°），连接BB1 ， 设CB1交AB于D，AlB1分别交AB，AC于E，F．

    (1)、求证：△BCD≌△A1CF；
    (2)、若旋转角α为30°，

    ①请你判断△BB1D的形状；

    ②求CD的长．

    查看试题解析

  • 23. 如图，抛物线y=﹣x2+bx+c与x轴交于A、B两点，与y轴交于点C，已知A（﹣1，0），C（0，3）

    (1)、求该抛物线的表达式；
    (2)、求BC的解析式；
    (3)、点M是对称轴右侧点B左侧的抛物线上一个动点，当点M运动到什么位置时，△BCM的面积最大？求△BCM面积的最大值及此时点M的坐标．

    查看试题解析