湖北省武汉市洪山区2018届九年级上学期数学期中考试试卷
试卷更新日期：2019-01-24 类型：期中考试
一、单选题
-
1. 一元二次方程x2+3x﹣a=0的一个根为﹣1，则另一个根为（ ）A、﹣2 B、2 C、4 D、﹣32. 已知x1、x2是一元二次方程x2﹣3x+2=0的两个实数根，则x1+x2等于（ ）A、﹣3 B、﹣2 C、2 D、33. 如图，一座石拱桥是圆弧形其跨度AB=24米，半径为13米，则拱高CD为（ ）
A、 3
米
B、5米
C、7米
D、8米
4. 将抛物线y=2（x+1）2﹣2的图象先向左平移1个单位长度，再向上平移3个单位长度，则顶点坐标为（ ）A、（﹣2，1） B、（2，1） C、（0，1） D、（﹣2，﹣5）5. 如图，在平面直角坐标系xOy中，△ABC顶点的横、纵坐标都是整数．若将△ABC以某点为旋转中心，顺时针旋转90°得到△DEF，则旋转中心的坐标是（ ）
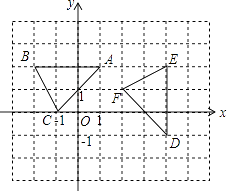A、（0，0） B、（1，0） C、（1，﹣1） D、（2.5，0.5）6. 用配方法解方程x2+6x+4=0，下列变形正确的是（ ）A、（x+3）2=﹣4 B、（x﹣3）2=4 C、（x+3）2=5 D、 （x+3）2=±
7. 今年某区积极推进“互联网+享受教育”课堂生态重构，加强对学校教育信息化的建设的投入，计划从今年起三年共投入1440万元，已知2015年投入1000万元．设投入经费的年平均增长率为x，根据题意，下面所列方程正确的是（ ）A、1000（1+x）2=1440 B、1000（x2+1）=1440 C、1000+1000x+1000x2=1440 D、1000+1000（1+x）+1000（1+x）2=14408. 已知点A（﹣3，y1），B（﹣1，y2），C（2，y3）在函数y=﹣x2﹣2x+b的图象上，则y1、y2、y3的大小关系为（ ）A、y1＜y3＜y2 B、y3＜y1＜y2 C、y3＜y2＜y1 D、y2＜y1＜y39. 如图，AB为⊙O的直径，点C、D在⊙O上，若∠AOD=30°，则∠BCD的度数是（ ）
A、150° B、120° C、105° D、75°10. 如图，在等腰Rt△ABC中，斜边AB=8，点P在以AC为直径的半圆上，M为PB的中点，当点P沿半圆从点A运动至点C时，点M运动的路径长是（ ）
A、 2
π
B、 π
C、2π
D、 2
二、填空题
-
11. 已知点P的坐标是（2，﹣3），那么点P关于原点的对称点P1的坐标是 ．12. 一次会议上，每两个参加会议的人都相互握一次手，有人统计一共握了36次手，设到会的人数为x人，则根据题意列方程为 ．13. 若二次函数y=（k﹣2）x2+2x+1的图象与x轴有交点，则k的取值范围是 ．14. 在△ABC中，∠A=120°，若BC=12，则其外接圆O的直径为 ．15. 如图，点P是等边三角形ABC内一点，且PA=3，PB=4，PC=5，若将△APB绕着点B逆时针旋转后得到△CQB，则∠APB的度数 ．
16. 直线y=m是平行于X轴的直线，将抛物线y=－ x2-4x在直线y=m上侧的部分沿直线 y=m翻折，翻折后的部分与没有翻折的部分组成新的函数图象，若新的函数图象刚好与 直线y=－x有3个交点，则满足条件的m 的值为三、解答题
-
17. 解方程：x2﹣2x﹣2=0．
18. 某新建火车站站前广场有一块长为20米，宽为8米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56米2 ， 两块绿地之间及周边留有宽度相等的人行通道（如图所示），问人行通道的宽度是多少米？
19. 如图，AB为⊙O的直径，弦CD⊥AB于E，∠CDB=15°，OE=2 ．
(1)、求⊙O的半径；(2)、将△OBD绕O点旋转，使弦BD的一个端点与弦AC的一个端点重合，则弦BD与弦AC的夹角为 ．20. 已知抛物线y=x2﹣2mx+m2﹣1（m是常数）的顶点为P，直线l：y=x﹣1．(1)、求证：点P在直线l上．(2)、若抛物线的对称轴为x=﹣3，直接写出该抛物线的顶点坐标 ， 与x轴交点坐标为 ．(3)、在（2）条件下，抛物线上点（﹣2，b）在图象上的对称点的坐标是 ．21. 如图，二次函数y= x2（0≤x≤2）的图象记为曲线C1 ， 将C1绕坐标原点O逆时针旋转90°，得曲线C2
(1)、请画出C2；(2)、写出旋转后A（2，5）的对应点A1的坐标；(3)、直接写出C1旋转至C2过程中扫过的面积．22. 如图，D为Rt△ABC斜边AB上一点，以CD为直径的圆分别交△ABC三边于E、F、G三点，连接FE，FG．
(1)、求证：∠EFG=∠B；(2)、若AC=2BC=4 ，D为AE的中点，求FG的长．23. 为了美化环境，学校准备在如图所示的矩形ABCD空地上进行绿化，规划在中间的一块四边形MNQP上种花，其余的四块三角形上铺设草坪，要求AM=AN=CP=CQ，已知BC=24米，AB=40米，设AN=x米，种花的面积为y1平方米，草坪面积y2平方米．
(1)、分别求y1和y2与x之间的函数关系式（不要求写出自变量的取值范围）；(2)、当AN的长为多少米时，种花的面积为440平方米？(3)、若种花每平方米需200元，铺设草坪每平方米需100元，现设计要求种花的面积不大于440平方米，设学校所需费用W（元），求W与x之间的函数关系式，并求出学校所需费用的最大值．24. 如图，抛物线y=ax2+2ax+c的图象与x轴交于A、B两点（点A在点B的左边）AB=4，与y轴交于点C，OC=OA，点D为抛物线的顶点．
(1)、求抛物线的解析式；(2)、点M（m，0）为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，可得矩形PQNM，如图1，点P在点Q左边，当矩形PQNM的周长最大时，求m的值，并求出此时的△AEM的面积；(3)、已知H（0，﹣1），点G在抛物线上，连HG，直线HG⊥CF，垂足为F，若BF=BC，求点G的坐标．