湖北省武汉市汉阳区2018届九年级上学期数学期中考试试卷
试卷更新日期：2019-01-24 类型：期中考试
一、单选题
-
1. 将一元二次方程3x2+1=6x化为一般形式后，常数项为1，二次项系数和一次项系数分别为（ ）A、3，﹣6 B、3，6 C、3，1 D、3x2 ， ﹣6x2. 用配方法解方程x2+10x+9=0，下列变形正确的是（ ）A、（x+5）2=16 B、（x+10）2=91 C、（x﹣5）2=34 D、（x+10）2=1093. 下面四个手机应用软件图标中是轴对称图形的是 （ ）.A、
B、
C、
D、
4. 下列方程中，没有实数根的方程式（ ）A、x2=9 B、4x2=3（4x﹣1） C、x（x+1）=1 D、2y2+6y+7=05. 二次函数 的图象是一条抛物线，下列关于该抛物线的说法正确的是（ ）A、抛物线开口向下 B、抛物线经过点（2，3） C、抛物线的对称轴是直线x=1 D、抛物线与x轴有两个交点6. 商品原价289元，经连续两次降价后售价为256元，设平均每次降价的百分率为x，则下面所列方程正确的是（ ）A、 289(1-
)2=256
B、 256(1- )2=289
C、 289(1-2 )=256
D、 256(1-2 )=289
7. 如图，在平面直角坐标系中，抛物线y=ax2+bx+5经过A（2，5），B（﹣1，2）两点，若点C在该抛物线上，则C点的坐标可能是（ ）
A、（﹣2，0） B、（0.5，6.5） C、（3，2） D、（2，2）8. 已知方程x2+bx+c=0有两个相等的实数根，且当x=a与x=a+n时，x2+bx+c=m，则m、n的关系为（A、 m= n B、 m= n C、 m= n2 D、 m= n29. 如图，一场篮球赛中，篮球运动员跳起投篮，已知球出手时离地面高2.2m，与篮圈中心的水平距离为8m，当球出手后水平距离为4m时达到最大高度4m，篮圈运行的轨迹为抛物线的一部分，篮圈中心距离地面3m，运动员发现未投中，若假设出手的角度和力度都不变，要使此球恰好通过篮圈中心，运动员应该跳得（ ）
A、比开始高0.8m B、比开始高0.4m C、比开始低0.8m D、比开始低0.4m二、填空题
-
10. 已知点P（2，﹣3）关于原点对称的点的坐标是 ．11. 将抛物线y=﹣x2向右平移3个单位后所得抛物线解析式的一般式为 ．12. 如图，用篱笆靠墙围成矩形花圃ABCD，墙可利用的最大长度为15m，一面利用旧墙，其余三面用篱笆围，篱笆长为24m，若围成的花圃面积为40m2时，平行于墙的BC边长为m．
13. 在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，以PB为边作等边△PBM，则线段AM的长最大值为 ．三、解答题
-
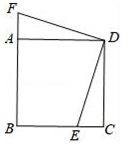
14. 解方程：x2＋3x－1=015. 如图，正方形ABCD中，E为BC边上一点，F为BA延长线上一点，且CE=AF．连接DE、DF．求证：DE=DF．
16. 已知y是x的函数，自变量x的取值范围x＞0，下表是y与x的几组对应值：
小腾根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．
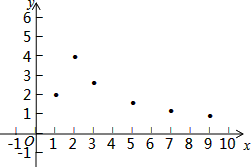
下面是小腾的探究过程，请补充完整：
(1)、如图，在平面直角坐标系xOy中，描出了以上表格中各对对应值为坐标的点，根据描出的点，画出该函数的图象；(2)、根据画出的函数图象，写出：①x=4对应的函数值y约为；
②该函数的一条性质： ．
17. 关于x的一元二次方程x2＋(2k＋1)x＋k2＋1＝0有两个不等实根x1 ， x2.(1)、求实数k的取值范围；(2)、若方程两实根x1 ， x2满足|x1|＋|x2|＝x1·x2 ， 求k的值．18. 如图，在△ABC中，AB=5，AC=13，边BC上的中线AD=6．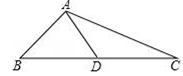
(1)、以点D为对称中心，作出△ABD的中心对称图形；(2)、求点A到BC的距离．19. 某商场销售一种产品，每件产品的成本为2400元，销售单价定位3000元，该商场为了促销，规定客户一次购买这种新型产品不超过10件时，每件按3000元销售；若一次购买该种产品超过10件时，每多购买一件，所购买的全部产品的销售单价均降低10元，但销售单价均不低于2600元；(1)、设一次购买这种产品x（x≥10）件，商场所获的利润为y元，求y（元）与x（件）之间的函数关系式，并写出自变量x的取值范围；(2)、在客户购买产品的件数尽可能少的前提下，商场所获的利润为12000元，此时该商场销售了多少件产品？(3)、填空：该商场的销售人员发现，当客户一次购买产品的件数在某一个区间时，会出现随着一次购买的数量的增多，商场所获的利润反而减少这一情况，客户一次购买产品的数量x满足的条件是 （其它销售条件不变）20. 已知在△ABC中，∠BAC=60°，点P为边BC的中点，分别以AB和AC为斜边向外作Rt△ABD和Rt△ACE，且∠DAB=∠EAC=α，连结PD，PE，DE．
(1)、如图1，若α=45°，则 =(2)、如图2，若α为任意角度，求证：∠PDE=α；(3)、如图3，若α=15°，AB=8，AC=6，则△PDE的面积为21. 如图，将函数y=x2﹣2x（x≥0）的图象沿y轴翻折得到一个新的图象，前后两个图象其实就是函数y=x2﹣2|x|的图象．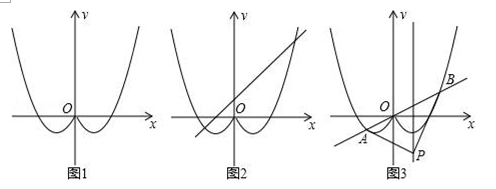
(1)、观察思考函数图象与x轴有个交点，所以对应的方程x2﹣2|x|=0有个实数根；方程x2﹣2|x|=2有个实数根；关于x的方程x2﹣2|x|=a有4个实数根时，a的取值范围是；
(2)、拓展探究①如图2，将直线y=x+1向下平移b个单位，与y=x2﹣2|x|的图象有三个交点，求b的值；
②如图3，将直线y=kx（k＞0）绕着原点旋转，与y=x2﹣2|x|的图象交于A、B两点（A左B右），直线x=1上有一点P，在直线y=kx（k＞0）旋转的过程中，是否存在某一时刻，△PAB是一个以AB为斜边的等腰直角三角形（点P、A、B按顺时针方向排列）．若存在，请求出k值；若不存在，请说明理由．