湖北省武汉市2018届九年级上学期数学期中考试试卷
试卷更新日期：2019-01-24 类型：期中考试
一、单选题
-
1. 方程（m－1）x²+2x+3=0是关于x的一元二次方程，则m的取值范围为（ ）A、m≠－1 B、m≠1 C、m≠2 D、m≠32. 在正方形、等腰三角形、矩形、菱形中，既是中心对称图形又是轴对称图形的有（ ）A、1个 B、2个 C、3个 D、4个3. 如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（ ）
A、30° B、40° C、50° D、65°4. 如图，AB是⊙O的直径，C，D是⊙O上的两点．若∠CAB=24°，则∠ADC的度数为（ ）
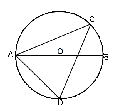A、45° B、60° C、66° D、70°5. 将抛物线y=x²－2x+3向上平移2个单位长度，再向左平移3个单位长度后，得到的抛物线的解析式为（ ）A、y=（x+2）²+4 B、y=（x－4）²+4 C、y=（x+2）² D、y=（x－4）²+66. 已知二次函数y＝x2－3x＋m的图象与x轴的一个交点坐标为(1，0)， 则关于x的一元二次方程x2－3x＋m＝0的两实数根是（ ）A、x1＝1，x2＝－1 B、x1＝1，x2＝2 C、x1＝1，x2＝0 D、x1＝1，x2＝37. 若抛物线y＝ax2＋bx＋c与x轴相交于A(x1 ， 0)，B(x2 ， 0)两点（点A在点B的左边），在x轴下方的抛物线上有一点M，其横坐标为x0 ， 则下列判断正确的是（ ）A、a＞0 B、b2－4ac<0 C、x1＜x0＜x2 D、a(x0－x1)(x0－x2)＜08. 已知抛物线y＝ax2＋bx＋c(a<0)过A(－2，0)，O(0，0），B(－3，y1)，C(3，y2)四点，则y1 与y2的大小关系是（ ）A、y1＞y2 B、y1=y2 C、y1＜y2 D、不能确定9. 如图，四边形ABCD为⊙O的内接四边形．延长AB与DC相交于点G，AO⊥CD，垂足为E，连接BD，∠GBC=50°，则∠DBC的度数为（ ）
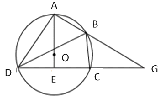A、50° B、60° C、75° D、80°10. 已知开口向上的抛物线y＝ax2＋bx＋c，它与x轴的两个交点分别为（－1，0），（3，0）．对于下列命题：①b－2a=0；②abc>0；③a－2b＋4c＜0；④8a＋c＞0．其中正确的有（ ）A、3个 B、2个 C、1个 D、0个二、填空题
-
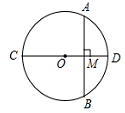
11. 已知点A与点B关于原点O的对称，若点A的坐标为（－3，2），则点B的坐标为 ．12. 若x=－2是关于x的方程x2－2ax+8=0的一个根，则a= ．13. 如图，CD为⊙O的直径，弦AB⊥CD，垂足为M，若AB=12，OM：MD=5：8，则⊙O的半径为 ．
14. 若抛物线y=mx2+mx-2与x轴只有一个交点，则m= ．15. 对于关于x的二次函数y＝x2－2mx－3，有下列说法：① 它的图象与x轴有两个公共点； ② 如果当x≤1时y随x的增大而减小，则m=1； ③ 如果将它的图象向左平移3个单位后过原点，则m=－1； ④ 如果当x=5时的函数值与x=2012时的函数值相等，则当x=2017时的函数值为－3．其中正确的说法有 ． （填序号）16. 若关于x的二次函数 的的图象与x轴的一个交点的坐标为（m，0），若1＜m＜3，则a的取值范围为 ．三、解答题
-
17. 解下列关于x的方程(1)、x2－4x－5＝0(2)、2x2－mx－1＝018. 已知抛物线y＝x2＋bx＋c经过点A(2，－3)，B(4，5).(1)、求抛物线的解析式；(2)、直接写出抛物线的对称轴和顶点坐标.19. 已知线段AB两个端点的坐标分别为A（1，－1），B（3，1），将线段AB绕点O逆时针旋转90°到对应线段CD（点A与点C对应，点B与点D对应）．(1)、直接写出C，D两点的坐标；(2)、点P在x轴上，当△PCD的周长最小时，直接写出点P的坐标．20. 求证：矩形的四个顶点在同一圆上.21. 如图，已知抛物线y＝－x2＋bx＋c与x轴负半轴交于点A，与y轴正半轴交于点B，且OA＝OB.
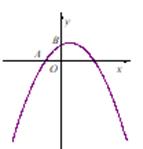(1)、求b＋c的值；(2)、若点C在抛物线上，且四边形OABC是平行四边形，求抛物线的解析式；(3)、在（2）条件下，点P（不与A，C重合）是抛物线上的一点，点M是y轴上一点，当△BPM是等腰直角三角形时，直接写出点M的坐标..22. 如图，已知锐角△ABC内接于⊙O，连接AO并延长交BC于点D．
(1)、求证：∠ACB+∠BAD=90°；(2)、过点D作DE⊥AB于E，若∠ADC=2∠ACB．求证：AC=2DE.23. 已知在平面直角坐标系中，直线y＝kx＋5与x轴交于点A，与抛物线y＝ax2＋bx交于B，C两点，且点B的坐标为（1，7），点C的横坐标为5.(1)、直接写出k的值和点C的坐标；(2)、将此抛物线沿对称轴向下平移n个单位，当抛物线与直线AB只有一个公共点时，求n的值；(3)、在抛物线上有点P，满足直线AB，AP关于x轴对称，求点P的坐标.．24. 如图1，抛物线y=ax2-4ax+b交x轴正半轴于A，B两点，交y轴正半轴于C，且OB=OC=3．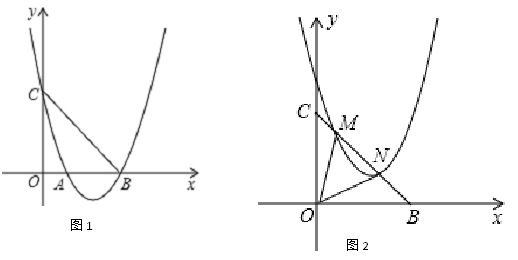
(1)、求抛物线的解析式；(2)、点D为抛物线的顶点，点G在直线BC上，若 ，直接写出点G的坐标；(3)、将抛物线向上平移m个单位，交BC于点M，N（如图2），若∠MON=45°，求m的值．