湖北省十堰市丹江口市2018届九年级上学期数学期中考试试卷
试卷更新日期:2019-01-24 类型:期中考试
一、单选题
-
1. 足球守门员大脚开出去的球的高度随时间的变化而变化,这一过程可近似地用下列哪幅图刻画( )A、
 B、
B、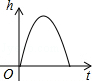 C、
C、 D、
D、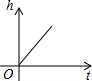 2. 对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )A、开口向下 B、对称轴是x=﹣1 C、顶点坐标是(1,2) D、与x轴有两个交点3. 将函数y=x2+6x+7进行配方正确的结果应为( )A、y=(x+3)2+2 B、y=(x-3)2+2 C、y=(x+3)2-2 D、y=(x-3)2-24. 如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
2. 对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )A、开口向下 B、对称轴是x=﹣1 C、顶点坐标是(1,2) D、与x轴有两个交点3. 将函数y=x2+6x+7进行配方正确的结果应为( )A、y=(x+3)2+2 B、y=(x-3)2+2 C、y=(x+3)2-2 D、y=(x-3)2-24. 如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )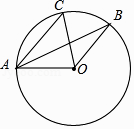 A、25° B、50° C、60° D、80°5. 如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为( )
A、25° B、50° C、60° D、80°5. 如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为( )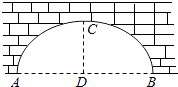 A、6.5米 B、9米 C、13米 D、15米6. 在 Rt△ABC 中,∠C=90°,BC=3cm,AC=4cm,以点C 为圆心,以2.5cm 为半径画圆,则⊙C与直线AB的位置关系是 ( )A、相交 B、相切 C、相离 D、不能确定7. 在抛物线y=ax2-2ax-3a上有A(-0.5,y1)、B(2,y2)和C(3,y3)三点,若抛物线与y轴的交点在正半轴上,则y1、y2和y3的大小关系为( )A、y3<y1<y2 B、y3<y2<y1 C、y2<y1<y3 D、y1<y2<y38. 某中学课外兴趣活动小组准备围建一个矩形苗圃圆,其中一边靠墙,另外三边用长为40米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米,围成的苗圃面积为y,则y关于x的函数关系式为( )
A、6.5米 B、9米 C、13米 D、15米6. 在 Rt△ABC 中,∠C=90°,BC=3cm,AC=4cm,以点C 为圆心,以2.5cm 为半径画圆,则⊙C与直线AB的位置关系是 ( )A、相交 B、相切 C、相离 D、不能确定7. 在抛物线y=ax2-2ax-3a上有A(-0.5,y1)、B(2,y2)和C(3,y3)三点,若抛物线与y轴的交点在正半轴上,则y1、y2和y3的大小关系为( )A、y3<y1<y2 B、y3<y2<y1 C、y2<y1<y3 D、y1<y2<y38. 某中学课外兴趣活动小组准备围建一个矩形苗圃圆,其中一边靠墙,另外三边用长为40米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米,围成的苗圃面积为y,则y关于x的函数关系式为( ) A、y=x(40﹣x) B、y=x(18﹣x) C、y=x(40﹣2x) D、y=2x(40﹣2x)9. 已知二次函数y=kx2-6x-9的图象与x轴有两个交点,则k的取值范围为( )A、k>-1 B、k>-1且k≠0 C、k≥-1 D、k<-1且k≠010. 如图,AB为⊙O的直径,AB=AC,AC交⊙O于点E,BC交⊙O于点D,F为CE的中点,连接DF.给出以下五个结论:①BD=DC;②AD=2DF;③ ;④DF是⊙O的切线.其中正确结论的个数是:( )
A、y=x(40﹣x) B、y=x(18﹣x) C、y=x(40﹣2x) D、y=2x(40﹣2x)9. 已知二次函数y=kx2-6x-9的图象与x轴有两个交点,则k的取值范围为( )A、k>-1 B、k>-1且k≠0 C、k≥-1 D、k<-1且k≠010. 如图,AB为⊙O的直径,AB=AC,AC交⊙O于点E,BC交⊙O于点D,F为CE的中点,连接DF.给出以下五个结论:①BD=DC;②AD=2DF;③ ;④DF是⊙O的切线.其中正确结论的个数是:( )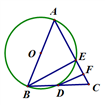 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴为直线x=1,若其与x轴一交点为A(3,0),则由图象可知,不等式ax2+bx+c<0的解集是 .
 12. 如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O,分别作AB、BC、AC的垂线,垂足分别为E、F、G,连接EF,若OG=3,则EF为 .
12. 如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O,分别作AB、BC、AC的垂线,垂足分别为E、F、G,连接EF,若OG=3,则EF为 . 13. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M的坐标为 .
13. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M的坐标为 .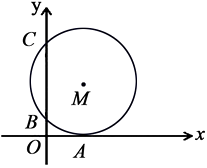 14. 若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移1个单位,再沿铅直方向向上平移3个单位,则原抛物线图象的解析式应变为.15. 如图,CA,CB分别切⊙O于点A,B,D为圆上不与A,B重合的一点,已知∠ACB=58°,则∠ADB的度数为 .
14. 若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移1个单位,再沿铅直方向向上平移3个单位,则原抛物线图象的解析式应变为.15. 如图,CA,CB分别切⊙O于点A,B,D为圆上不与A,B重合的一点,已知∠ACB=58°,则∠ADB的度数为 . 16. 二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:下列结论:①ac<0;②当x>1时,y的值随x的增大而减小;③3是方程ax2+(b﹣1)x+c=0的一个根;④当﹣1<x<3时,ax2+(b﹣1)x+x>0.其中正确的序号为
16. 二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:下列结论:①ac<0;②当x>1时,y的值随x的增大而减小;③3是方程ax2+(b﹣1)x+c=0的一个根;④当﹣1<x<3时,ax2+(b﹣1)x+x>0.其中正确的序号为x
﹣1
0
1
3
y
﹣1
3
5
3
三、解答题
-
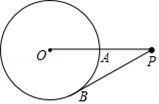
17. 已知抛物线y=x2﹣2x﹣8与x轴的两个交点为A,B(A在左边),且它的顶点为P.(1)、求A、B两点的坐标(2)、求△PAB的面积.18. 如图,P是⊙O外一点,OP交⊙O于A点,PB切⊙O于B点,已知OA=1,OP=2,求PB的长.
 19. 如图,△ABC内接于⊙O,∠A=45°,⊙O的半径为5,求BC的长.
19. 如图,△ABC内接于⊙O,∠A=45°,⊙O的半径为5,求BC的长. 20. 河上有一座桥孔为抛物线形的拱桥,水面宽为6米时,水面离桥孔顶部3米.把桥孔看成一个二次函数的图象,以桥孔的最高点为原点,过原点的水平线为横轴,过原点的铅垂线为纵轴,建立如图所示的平面直角坐标系.
20. 河上有一座桥孔为抛物线形的拱桥,水面宽为6米时,水面离桥孔顶部3米.把桥孔看成一个二次函数的图象,以桥孔的最高点为原点,过原点的水平线为横轴,过原点的铅垂线为纵轴,建立如图所示的平面直角坐标系. (1)、请求出这个二次函数的表达式;(2)、因降暴雨水位上升1米,此时水面宽为多少?21. 如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)、请求出这个二次函数的表达式;(2)、因降暴雨水位上升1米,此时水面宽为多少?21. 如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,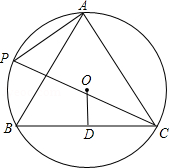 (1)、求证:△ABC是等边三角形;(2)、求圆心O到BC的距离OD.22. 已知抛物线y=x2-(m+1)x+m,(1)、求证:抛物线与x轴一定有交点;(2)、若抛物线与x轴交于A(x1 , 0),B(x2 , 0)两点,x1﹤0﹤x2 , 且 ,求m的值.23. 某商品的进价为每件20元,现在的售价为每件30元,每星期可卖出150件,市场调查反映:如果每件涨价1元(每件售价不能高于35元),那么每星期少卖10件,设每件涨价x元(x为非负整数),每星期销量为y件.(1)、求y关于x的函数解析式及自变量x的取值范围;(2)、如何定价才能使每星期的利润最大且每星期的销量较大?每星期的最大利润是多少?24. 如图①,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)、求证:△ABC是等边三角形;(2)、求圆心O到BC的距离OD.22. 已知抛物线y=x2-(m+1)x+m,(1)、求证:抛物线与x轴一定有交点;(2)、若抛物线与x轴交于A(x1 , 0),B(x2 , 0)两点,x1﹤0﹤x2 , 且 ,求m的值.23. 某商品的进价为每件20元,现在的售价为每件30元,每星期可卖出150件,市场调查反映:如果每件涨价1元(每件售价不能高于35元),那么每星期少卖10件,设每件涨价x元(x为非负整数),每星期销量为y件.(1)、求y关于x的函数解析式及自变量x的取值范围;(2)、如何定价才能使每星期的利润最大且每星期的销量较大?每星期的最大利润是多少?24. 如图①,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB. (1)、求证:BC为⊙O的切线;(2)、连接AE并延长与BC的延长线交于点G(如图②所示).若AB= ,CD=9,求线段BC和EG的长.25. 如图,在直角坐标系中,直线y=x-3交x轴于点B,交y轴于点C,抛物线经过点A(-1,0),B,C三点,点F在y轴负半轴上,OF=OA.
(1)、求证:BC为⊙O的切线;(2)、连接AE并延长与BC的延长线交于点G(如图②所示).若AB= ,CD=9,求线段BC和EG的长.25. 如图,在直角坐标系中,直线y=x-3交x轴于点B,交y轴于点C,抛物线经过点A(-1,0),B,C三点,点F在y轴负半轴上,OF=OA.
 (1)、求抛物线的解析式;(2)、在第一象限的抛物线上存在一点P,满足S△ABC=S△PBC , 请求出点P的坐标;(3)、点D是直线BC的下方的抛物线上的一个动点,过D点作DE∥y轴,交直线BC于点E,①当四边形CDEF为平行四边形时,求D点的坐标;
(1)、求抛物线的解析式;(2)、在第一象限的抛物线上存在一点P,满足S△ABC=S△PBC , 请求出点P的坐标;(3)、点D是直线BC的下方的抛物线上的一个动点,过D点作DE∥y轴,交直线BC于点E,①当四边形CDEF为平行四边形时,求D点的坐标;②是否存在点D,使CE与DF互相垂直平分?若存在,请求出点D的坐标;若不存在,请说明理由.