湖北省潜江市十校联考2018届九年级上学期数学期中考试试卷

试卷更新日期：2019-01-24 类型：期中考试

进入出卷网下载

一、单选题

1. 抛物线 $y = x^{2} - 4 x + m^{2} + 5$ （m是常数）的顶点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下面四个手机应用图标中，属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在⊙O中，弦AB的长为6，圆心O到AB的距离为4，则⊙O的半径为（）

A、10 B、6 C、5 D、4

查看试题解析
4. 若二次函数y=x²+mx的对称轴是x=3，则关于x的方程x²+mx=7的解为（　　）

A、x₁=0，x₂=6 B、x₁=1，x₂=7 C、x₁=1，x₂=﹣7 D、x₁=﹣1，x₂=7

查看试题解析
5. 下列说法正确的是（）

A、将抛物线向左平移4个单位后，再向下平移2个单位，则此时抛物线的解析式是y=（x－4）²-2 B、方程x²+2x+3=0有两个不相等的实数根 C、半圆是弧，但弧不一定是半圆． D、平分弦的直径垂直于弦，并且平分这条弦所对的两条弧

查看试题解析
6. 某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映，如果调整商品售价，每降价1元，每星期可多卖出20件．设每件商品降价x元后，每星期售出商品的总销售额为y元，则y与x的关系式为（　　）

A、y=60（300+20x） B、y=（60﹣x）（300+20x） C、y=300（60﹣20x） D、y=（60﹣x）（300﹣20x）

查看试题解析
7. 已知抛物线y=x²-2mx-4（m＞0）的顶点M关于坐标原点O的对称点为M′，若点M′在这条抛物线上，则点M的坐标为（）

A、（1，-5） B、（3，-13） C、（2，-8） D、（4，-20）

查看试题解析
8. 如图，在Rt△ABC中，∠ACB=90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，P是A'B'的中点，连接PM．若BC=2，∠BAC=30°，则线段PM的最大值是（）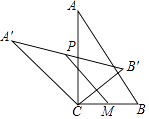

A、4 B、3 C、2 D、1

查看试题解析
9. 如图，抛物线y₁= $\frac{1}{2}$ （x+1）²+1与y₂=a（x﹣4）²﹣3交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于B、C两点，且D、E分别为顶点．则下列结论：
①a= $\frac{2}{3}$ ；②AC=AE；③△ABD是等腰直角三角形；④当x＞1时，y₁＞y₂
其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、解答题

10. 根据要求，解答下列问题．仔细观察小聪同学所求的三个方程的解．
①方程x²－2x＋1＝0的解为x₁＝1，x₂＝1；②方程x²－3x＋2＝0的解为x₁＝1，x₂＝2；③方程x²－4x＋3＝0的解为x₁＝1，x₂＝3； …………

(1)、根据以上方程特征及其解的特征，请猜想：
①方程x²－9x＋8＝0的解为；

②关于x的方程的解为x₁＝1，x₂＝n．

(2)、请用配方法解方程x²－9x＋8＝0，以验证猜想结论的正确性．

查看试题解析
11.
已知：如图，AB是⊙O的直径，CD是⊙O的弦，AB，CD的延长线交于E，若AB=2DE，∠C=40°，求∠E及∠AOC的度数．

查看试题解析
12. 如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，2）请解答下列问题：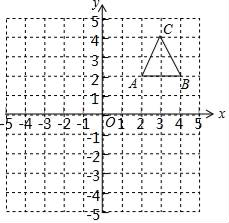

①画出△ABC关于y轴对称的△A₁B₁C₁ ，并写出A₁的坐标．

②画出△ABC绕点B逆时针旋转90°后得到的△A₂B₂C₂ ，并写出A₂的坐标．

③画出△A₂B₂C₂关于原点O成中心对称的△A₃B₃C₃ ，并写出A₃的坐标．

查看试题解析
13. 已知关于x的一元二次方程x²-6x+m+4=0有两个实数根x₁ ， x₂ ．

(1)、求m的取值范围；

(2)、若x₁ ， x₂满足3x₁=|x₂|+2，求m的值．

查看试题解析
14. 如图，有一座拱桥是圆弧形，它的跨度AB=60米，拱高PD=18米．

(1)、求圆弧所在的圆的半径r的长；

(2)、当洪水泛滥到跨度只有30米时，要采取紧急措施，若拱顶离水面只有4米，即PE=4米时，是否要采取紧急措施？

查看试题解析
15. 如图，已知抛物线y=﹣x²+mx+3与x轴交于点A、B两点，与y轴交于C点，点B的坐标为（3，0），抛物线与直线y=﹣ $\frac{3}{2}$ x+3交于C、D两点．连接BD、AD．

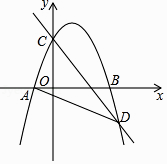(1)、求m的值．

(2)、抛物线上有一点P，满足S_△ABP=4S_△ABD ，求点P的坐标．

查看试题解析
16. 工人师傅用一块长为10dm，宽为6dm的矩形铁皮制作一个无盖的长方体容器，需要将四角各裁掉一个正方形．（厚度不计）

(1)、在图中画出裁剪示意图，用实线表示裁剪线，虚线表示折痕；并求长方体底面面积为12dm²时，裁掉的正方形边长多大？

(2)、若要求制作的长方体的底面长不大于底面宽的五倍，并将容器进行防锈处理，侧面每平方分米的费用为0.5元，底面每平方分米的费用为2元，裁掉的正方形边长多大时，总费用最低，最低为多少？

查看试题解析
17. 已知O为直线MN上一点，OP⊥MN，在等腰Rt△ABO中， $∠ B A O = 90 °$ ，AC∥OP交OM于C，D为OB的中点，DE⊥DC交MN于E．

(1)、如图1，若点B在OP上，则①ACOE(填“＜”，“＝”或“＞”)；②线段CA、CO、CD满足的等量关系式是；

(2)、将图1中的等腰Rt△ABO绕O点顺时针旋转a( $0 ° < α < 45 °$ )，如图2，那么(1)中的结论②是否成立？请说明理由；

(3)、将图1中的等腰Rt△ABO绕O点顺时针旋转a（），请你在图3中画出图形，并直接写出线段CA、CO、CD满足的等量关系式；

查看试题解析

三、填空题

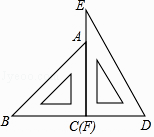
18. 若点M（3，a﹣2），N（b，a）关于原点对称，则a+b= ．

查看试题解析
19. 一副三角尺按如图的位置摆放（顶点C 与F 重合，边CA与边FE叠合，顶点B、C、D在一条直线上）．将三角尺DEF绕着点F按顺时针方向旋转n°后（0＜n＜180 ），如果EF∥AB，那么n的值是．

查看试题解析
20. 关于x的一元二次方程 $(a - 1) x^{2} + (2 a + 1) x + a = 0$ 有两个不相等的实数根，则a的取值范围是．

查看试题解析
21. 若将图中的抛物线y=x²-2x+c向上平移，使它经过点（2，0），则此时的抛物线位于x轴下方的图象对应x的取值范围是.

查看试题解析
22. 已知⊙O的半径为10，弦AB∥CD，AB=12，CD=16，则AB和CD的距离为．

查看试题解析