河南省南阳市镇平县2018届九年级上学期数学期中考试试卷

试卷更新日期：2019-01-24 类型：期中考试

进入出卷网下载

一、单选题

1. 化简 $\sqrt{12}$ 的结果是（）

A、 4 $\sqrt{3}$ B、 2 $\sqrt{3}$ C、 3 D、 2 $\sqrt{6}$

查看试题解析
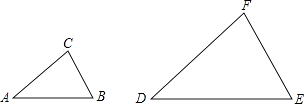
2. 如图，△ABC∽△DEF ，相似比为1：2．若BC=1，则EF的长是（　　）

A、1 B、2 C、3 D、4

查看试题解析
3. 设α，β是一元二次方程x²＋2x－1＝0的两个根，则αβ的值是（）

A、2 B、1 C、－2 D、－1

查看试题解析
4. 下列式子为最简二次根式的是（　　）.

A、 $\sqrt{3}$ B、 $\sqrt{4}$ C、 $\sqrt{8}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
5. 已知x=1是关于x的方程(1-k)x²+k²x-1=0的根，则常数k的值为（）

A、0 B、1 C、0或1 D、0或-1

查看试题解析
6. 如图，在平行四边形ABCD中，点E在边DC上，DE：EC=3：1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为（）

A、3：4 B、9：16 C、9：1 D、3：1

查看试题解析
7. 用配方法解一元二次方程x²+4x﹣5=0，此方程可变形为（　　）

A、（x+2）²=9 B、（x﹣2）²=9 C、（x+2）²=1 D、（x﹣2）²=1

查看试题解析
8. 如图，在平面直角坐标系中，正三角形OAB的顶点B的坐标为（2，0），点A在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3，则点B′的坐标为（）

A、（4，2 $\sqrt{3}$ ） B、（3，3 $\sqrt{3}$ ） C、（4，3 $\sqrt{3}$ ） D、（3，2 $\sqrt{3}$ ）

查看试题解析
9. 已知，直角坐标系中，点E（-4，2），F（-1，-1），以O为位似中心，按比例尺2：1把△EFO缩小，则点E的对应点 $E'$ 的坐标为（）

A、（2，-1）或（-2，1） B、（8，-4）或（-8，4） C、（2，-1） D、（8，-4）

查看试题解析

二、填空题

10. 计算 $\frac{\sqrt{5} \times \sqrt{15}}{\sqrt{3}}$ 的结果是 .

查看试题解析
11. 一元二次方程9（x﹣1）²﹣4=0的解是．

查看试题解析
12. 若 $\frac{m + n}{n} = \frac{5}{2}$ ，则 $\frac{m}{n}$ 等于．

查看试题解析
13. 已知k＞0，且关于x的方程3kx²+12x+k+1=0有两个相等的实数根，那么k的值等于．

查看试题解析
14. 如图，在平面直角坐标系中，将矩形AOCD沿直线AE折叠（点E在边DC上），折叠后顶点D恰好落在边OC上的点F处，已知AD=3，当点F为线段OC的三等分点时，点E的坐标为．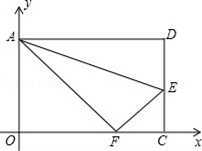

查看试题解析

三、解答题

15. 计算： $\sqrt{24}$ × $\sqrt{\frac{1}{3}}$ ﹣4× $\sqrt{\frac{1}{8}}$ ×（1﹣ $\sqrt{2}$ ）⁰ ．

查看试题解析
16. 用适当的方法解下列方程．

(1)、x²﹣x﹣1=0；

(2)、x²﹣2x=2x+1；

(3)、x（x﹣2）﹣3x²=﹣1；

(4)、（x+3）²=（1﹣2x）² ．

查看试题解析
17. 先化简，再求值：（ $\frac{a^{2} - b^{2}}{a^{2} - 2 a b + b^{2}} + \frac{a}{b - a}$ ）÷ $\frac{b^{2}}{a^{2} - a b}$ ，其中a，b满足 $\sqrt{a + 1}$ +|b﹣ $\sqrt{3}$ |=0．

查看试题解析
18. 如图，是一个照相机成像的示意图，像高MN，景物高度AB、CD为水平视线，根据物体成像原理知：AB∥MN，CD⊥MN．

(1)、如果像高MN是35mm，焦距CL是50mm，拍摄的景物高度AB是4.9m，拍摄点离景物的距离LD是多少？

(2)、如果要完整的拍摄高度是2m的景物，拍摄点离景物有4m，像高不变，则相机的焦距应调整为多少毫米？

查看试题解析
19. 已知关于x的方程（x﹣3）（x﹣2）﹣p²=0．

(1)、求证：方程总有两个不相等的实数根；

(2)、当p=2时，求该方程的根．

查看试题解析
20. 如图，在矩形ABCD中，已知AB=24，BC=12，点E沿BC边从点B开始向点C以每秒2个单位长度的速度运动；点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动，如果E、F同时出发，用t（0≤t≤6）秒表示运动的时间，当t为何值时，以点E、C、F为顶点的三角形与△ACD相似？

查看试题解析
21. 某商场礼品柜台春节期间购进大量贺年卡，一种贺年卡平均每天可售出500张，每张盈利0.3元，为了尽快减少库存，商场决定采取适当的降价措施，调查发现，如果这种贺年卡的售价每降低0.1元，那么商场平均每天可多售出100张．

(1)、填空：设每张贺年卡应降价x元，则每件平均利润应是元，总件数应是件；

(2)、商场要想平均每天盈利120元，每张贺年卡应降价多少元？

查看试题解析
22. 如图，在矩形ABCD中，AB=5，BC=3，将矩形ABCD绕点B旋转得到矩形GBEF．

(1)、观察发现：在旋转的过程中， $\frac{C E}{A G}$ 的值不变，这个数值是；

(2)、问题解决：当点G落在直线CD上时，求CE的长；

(3)、数学思考：在旋转的过程中，CE是否有最大值，如果有，请直接写出；如果没有，试说明理由．

查看试题解析