2016-2017学年河南省濮阳市八年级上学期期末数学试卷

试卷更新日期：2017-04-14 类型：期末考试

进入出卷网下载

一、选择题：

1. 下列长度的三条线段能组成三角形的是（）

A、2，3，4 B、3，3，6 C、1，2，3 D、5，10，4

查看试题解析
2. 已知等腰三角形的一个内角是70°，则这个等腰三角形的顶角为（）

A、70° B、40° C、70°或40° D、以上答案都不对

查看试题解析
3. 设点M（x，y）在第二象限，且|x|=2，|y|=3，则点M关于y轴的对称点的坐标是（）

A、（2，3） B、（﹣2，3） C、（﹣3，2） D、（﹣3，﹣2）

查看试题解析
4. 下列运算正确的是（）

A、a⁴•a²=a⁸ B、a⁵+a⁵=a¹⁰ C、（﹣3a³）²=6a⁶ D、（a³）²•a=a⁷

查看试题解析
5. 若分式： $\frac{x^{2} - 1}{x - 1}$ 的值为0，则（）

A、x=1 B、x=﹣1 C、x=±1 D、x≠1

查看试题解析
6. 下列图形中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
7. 下列式子中，从左到右的变形是因式分解的是（　　）

A、（x﹣1）（x﹣2）=x²﹣3x+2 B、x²﹣3x+2=（x﹣1）（x﹣2） C、x²+4x+4=x（x﹣4）+4 D、x²+y²=（x+y）（x﹣y）

查看试题解析
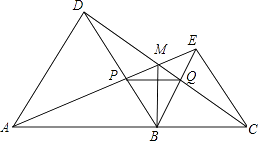
8. 如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，下面结论：
①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④PQ∥AC．
其中结论正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题：

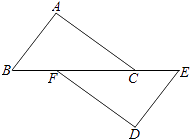
9. 5.8×10^﹣⁵的原数是．

查看试题解析
10. 若25x²+kxy+4y²是一个完全平方式，则k= ．

查看试题解析
11. 已知一个多边形的内角和是外角和的 $\frac{3}{2}$ ，则这个多边形的边数是．

查看试题解析
12. 分解因式：a³b﹣9ab= ．

查看试题解析
13. 如图，在△ABC和△DEF中，点B、F、C、E在同一直线上，BF=CE，AC∥DF，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是．（只需写一个，不添加辅助线）

查看试题解析
14. 如图所示，在△ABC中，AB=AC，DE是AB的垂直平分线，△BCE的周长为14cm，BC=6cm，则AB= ．

查看试题解析
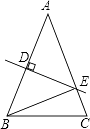15. 求2¹+2²+2³+…+2ⁿ的和，解法如下：
解：设S=2¹+2²+2³+…+2ⁿ①
2S=2²+2³+…+2ⁿ+2ⁿ⁺¹②
②﹣①得S=2ⁿ⁺¹﹣2
所以2¹+2²+2³+…+2ⁿ=2ⁿ⁺¹﹣2
参照上面的解法，
计算：1+3¹+3²+3³+…+3ⁿ^﹣¹= ．

查看试题解析

三、解答题：

16. 先化简再求值：（ $\frac{x + 2}{x^{2} - 2 x}$ ﹣ $\frac{x - 1}{x^{2} - 4 x + 4}$ ）÷ $\frac{x - 4}{x}$ ，其中x=1．

查看试题解析
17. 如图，BD是∠ABC的平分线，DE⊥AB于E，△ABC的面积为36cm² ， AB=18cm，BC=12cm，求DE的长．

查看试题解析
18.
如图，在平面直角坐标系xOy中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．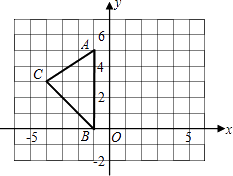

(1)、求出△ABC的面积．

(2)、在图中作出△ABC关于y轴的对称图形△A₁B₁C₁ ．

(3)、写出点A₁ ， B₁ ， C₁的坐标．

查看试题解析
19. 如图，在△ABC中，D是BC的中点，过点D的直线GF交AC于点F，交AC的平行线BG于点G，DE⊥DF交AB于点E，连接EG、EF．

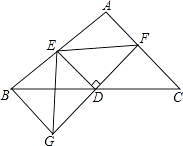(1)、求证：BG=CF；

(2)、求证：EG=EF；

(3)、请你判断BE+CF与EF的大小关系，并证明你的结论．

查看试题解析
20. 小刚的妈妈在百姓量贩用12.50元买了若干瓶酸奶，但她在普客隆超市内发现，同样的酸奶，这里要比百姓量贩每瓶便宜0.2元；因此，但第二次买酸奶时，她便到普客隆超市去买，结果用去18.40元钱，买的瓶数比第一次买的瓶数多 $\frac{3}{5}$ ，问：她第一次在百姓量贩买了几瓶酸奶？

查看试题解析
21. 从边长为a的正方形中剪掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．

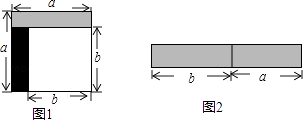(1)、上述操作能验证的等式是；（请选择正确的一个）

A、a²﹣2ab+b²=（a﹣b）² B、a²﹣b²=（a+b）（a﹣b） C、a²+ab=a（a+b）

(2)、应用你从（1）选出的等式，完成下列各题：
①已知x²﹣4y²=12，x+2y=4，求x﹣2y的值．
②计算：（1﹣ $\frac{1}{2^{2}}$ ）（1﹣ $\frac{1}{3^{2}}$ ）（1﹣ $\frac{1}{4^{2}}$ ）…（1﹣ $\frac{1}{19^{2}}$ ）（1﹣ $\frac{1}{20^{2}}$ ）．

查看试题解析
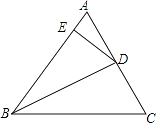
22. 如图，在Rt△ABC中，∠C=90°，∠A=60°，AB=12cm，若点P从点B出发以2cm/s的速度向点A运动，点Q从点A出发以1cm/s的速度向点C运动，设P、Q分别从点B、A同时出发，运动的时间为ts．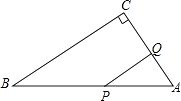

(1)、用含t的式子表示线段AP、AQ的长；

(2)、当t为何值时，△APQ是以PQ为底边的等腰三角形？

(3)、当t为何值时，PQ∥BC？

查看试题解析
23. 在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．

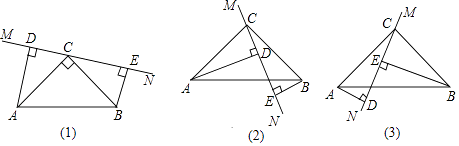(1)、当直线MN绕点C旋转到图（1）的位置时，
求证：①△ADC≌△CEB．②DE=AD+BE；

(2)、当直线MN绕点C旋转到图（2）的位置时，求证：DE=AD﹣BE；

(3)、当直线MN绕点C旋转到图（3）的位置时，请直接写出DE，AD，BE之间的等量关系．

查看试题解析