湖北省宜昌市点军区2018届九年级上学期数学期中考试试卷
试卷更新日期:2019-01-24 类型:期中考试
一、单选题
-
1. 下列汽车标志中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程 的二次项系数和一次项系数分别为 ( )A、3,-1 B、3,-4 C、3,4 D、 ,
2. 一元二次方程 的二次项系数和一次项系数分别为 ( )A、3,-1 B、3,-4 C、3,4 D、 , 3. 若 是关于 的一元二次方程 的一个根,则 的值是( )A、 B、0 C、1 D、无法确定4. 若 为方程 的解,则 的值为( )A、 B、16 C、9 D、65. 方程 的解是( )A、
3. 若 是关于 的一元二次方程 的一个根,则 的值是( )A、 B、0 C、1 D、无法确定4. 若 为方程 的解,则 的值为( )A、 B、16 C、9 D、65. 方程 的解是( )A、 B、
C、
B、
C、 D、
6. 关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是( )A、
D、
6. 关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是( )A、 B、
B、 C、
C、 D、
D、 7. 若m、n是一元二次方程x2﹣5x﹣2=0的两个实数根,则m+n﹣mn的值是( )A、﹣7 B、7 C、3 D、﹣38. 抛物线 的顶点坐标是( )A、(2, 1) B、(-2, 1) C、(2, -1) D、(-2, -1)9. 抛物线 向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )A、
7. 若m、n是一元二次方程x2﹣5x﹣2=0的两个实数根,则m+n﹣mn的值是( )A、﹣7 B、7 C、3 D、﹣38. 抛物线 的顶点坐标是( )A、(2, 1) B、(-2, 1) C、(2, -1) D、(-2, -1)9. 抛物线 向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )A、 B、
B、 C、
C、 D、
D、 10. ⊙O的直径为10,圆心O到弦AB的距离为3,则弦AB的长是( )A、4 B、6 C、7 D、811. 如图,矩形OABC的顶点O为坐标原点,点A在x轴上,点B的坐标为(2,1).如果将矩形OABC绕点O顺时针旋转180°,旋转后的图形为矩形OA1B1C1 , 那么点B1的坐标为( )
10. ⊙O的直径为10,圆心O到弦AB的距离为3,则弦AB的长是( )A、4 B、6 C、7 D、811. 如图,矩形OABC的顶点O为坐标原点,点A在x轴上,点B的坐标为(2,1).如果将矩形OABC绕点O顺时针旋转180°,旋转后的图形为矩形OA1B1C1 , 那么点B1的坐标为( ) A、(2,1) B、(-2,1) C、(-2,-1) D、(2,-1)12. 如图,△OAB绕点O逆时针旋转70°得到△OCD,若∠A=110°, ∠D=30°,则∠α的度数是( )
A、(2,1) B、(-2,1) C、(-2,-1) D、(2,-1)12. 如图,△OAB绕点O逆时针旋转70°得到△OCD,若∠A=110°, ∠D=30°,则∠α的度数是( ) A、20° B、30° C、40° D、50°13. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则当函数值y>0时,x的取值范围是 ( )
A、20° B、30° C、40° D、50°13. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则当函数值y>0时,x的取值范围是 ( ) A、x<-1 B、x>3 C、-1<x<3 D、x<-1或x>314. 制造一种产品,原来每件的成本是100元,由于连续两次降低成本,现在的成本是81元,则平均每次降低成本的百分率为( ).A、2 0% B、15% C、10% D、5%15. 在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )A、
A、x<-1 B、x>3 C、-1<x<3 D、x<-1或x>314. 制造一种产品,原来每件的成本是100元,由于连续两次降低成本,现在的成本是81元,则平均每次降低成本的百分率为( ).A、2 0% B、15% C、10% D、5%15. 在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )A、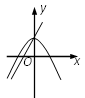 B、
B、 C、
C、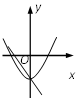 D、
D、
二、解答题
-
16. 解方程:x2-3x-1=0.17. 如图,⊙O的直径AB垂直于弦CD,垂足P是OB的中点,CD=6cm,求直径AB的长.
 18. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,0)、B(4,0)、C(5,2).将△ABC绕着点A按逆时针方向旋转90度得到△A1B1C1
18. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,0)、B(4,0)、C(5,2).将△ABC绕着点A按逆时针方向旋转90度得到△A1B1C1 (1)、请画出△A1B1C1;(2)、写出点B1 、C1的坐标.19. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
(1)、请画出△A1B1C1;(2)、写出点B1 、C1的坐标.19. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
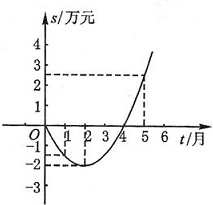 (1)、由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;(2)、求截止到几月末公司累积利润可达到30万元;(3)、求第8个月公司所获利润为多少万元?20. 如图,点O是等边 △ABC 内一点, .将 △BOC 绕点 C 按顺时针方向旋转 得 △ADC ,连接OD.
(1)、由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;(2)、求截止到几月末公司累积利润可达到30万元;(3)、求第8个月公司所获利润为多少万元?20. 如图,点O是等边 △ABC 内一点, .将 △BOC 绕点 C 按顺时针方向旋转 得 △ADC ,连接OD. (1)、求证: 是等边三角形;(2)、当 时,试判断 的形状,并说明理由;21. 如图,某单向行驶隧道横截面上的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成.矩形的长是12米,宽是3米,隧道的最大高度为6米,现以O点为原点,OM所在直线为x轴建立直角坐标系.
(1)、求证: 是等边三角形;(2)、当 时,试判断 的形状,并说明理由;21. 如图,某单向行驶隧道横截面上的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成.矩形的长是12米,宽是3米,隧道的最大高度为6米,现以O点为原点,OM所在直线为x轴建立直角坐标系.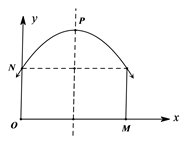 (1)、直接写出点M、点N及抛物线顶点P的坐标;(2)、求出这条抛物线的函数解析式;(3)、一大货运汽车装载某大型设备后高为5米,宽为4米,那么这辆货车能否安全通过?22. “中国梦,点军梦”,2017年9月1日点军区某校新校区一期工程通过工程竣工验收全面投入使用。该校区一期工程自2015年年初开始投资建设,工程分别由搬迁安置、工程建设、辅助配套三项工程组成,市政府在每年年初分别对三项工程进行不同数额的投资。2015年年初共投资9亿元,其中对工程建设、辅助配套的投资分别是搬迁安置投资的3倍、5倍。随后两年,搬迁安置投资每年都增加相同的数额,辅助配套投资从2016年初开始遂年按同一百分数递减;2016年年初工程投资数额正好是搬迁安置投资每年增加数额的2倍, 2017年年初工程投资数额较前一年的增长率正好是2016年初辅助配套投资遂年递减百分率的2.5倍。工程结束后经核算,这三年的搬迁安置总投资达6亿元,且三年的搬迁安置与辅助配套总投资之和比工程建设总投资还多10.2亿元。
(1)、直接写出点M、点N及抛物线顶点P的坐标;(2)、求出这条抛物线的函数解析式;(3)、一大货运汽车装载某大型设备后高为5米,宽为4米,那么这辆货车能否安全通过?22. “中国梦,点军梦”,2017年9月1日点军区某校新校区一期工程通过工程竣工验收全面投入使用。该校区一期工程自2015年年初开始投资建设,工程分别由搬迁安置、工程建设、辅助配套三项工程组成,市政府在每年年初分别对三项工程进行不同数额的投资。2015年年初共投资9亿元,其中对工程建设、辅助配套的投资分别是搬迁安置投资的3倍、5倍。随后两年,搬迁安置投资每年都增加相同的数额,辅助配套投资从2016年初开始遂年按同一百分数递减;2016年年初工程投资数额正好是搬迁安置投资每年增加数额的2倍, 2017年年初工程投资数额较前一年的增长率正好是2016年初辅助配套投资遂年递减百分率的2.5倍。工程结束后经核算,这三年的搬迁安置总投资达6亿元,且三年的搬迁安置与辅助配套总投资之和比工程建设总投资还多10.2亿元。求:
(1)、2015年年初工程建设投资是多少亿元?(2)、市政府三年建设总投资是多少亿元?23. 如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM⊥直线a于点M,CN⊥直线a于点N,连接PM、PN; (1)、延长MP交CN于点E(如图2)。j求证:△BPM≌△CPE;k求证:PM=PN;(2)、若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)、若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN
(1)、延长MP交CN于点E(如图2)。j求证:△BPM≌△CPE;k求证:PM=PN;(2)、若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)、若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由。
24. 已知抛物线 ,其中 .(1)、直接写出关于 的一元二次方程 的两个根; (2)、试判断:抛物线 的顶点 在第几象限内;(3)、过点A的直线y=x+m与抛物线 相交于另一点B,抛物线 的对称轴与x轴相交于C.试问:在抛物线上是否存在一点D,使 ?若存在,求抛物线的表达式,若不存在,说明理由。
(2)、试判断:抛物线 的顶点 在第几象限内;(3)、过点A的直线y=x+m与抛物线 相交于另一点B,抛物线 的对称轴与x轴相交于C.试问:在抛物线上是否存在一点D,使 ?若存在,求抛物线的表达式,若不存在,说明理由。