湖北省宜昌市东部2017-2018学年八年级上学期数学期中考试试卷
试卷更新日期：2019-01-24 类型：期中考试
一、单选题
-
1. 下列大学的校徽图案是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列图形不具有稳定性的是（ ）A、正方形 B、等腰三角形 C、直角三角形 D、钝角三角形3. 若△ABC内一点O到三角形三条边的距离相等，则O为△ABC（ ）的交点．A、角平分线 B、高线 C、中线 D、边的中垂线4. 王老师一块教学用的三角形玻璃不小心打破了，他想再到玻璃店划一块同样大小的三角形玻璃，为了方便他只要带哪一块就可以（ ）
A、③ B、② C、① D、都不行5. 已知图中的两个三角形全等，则∠1等于（ ）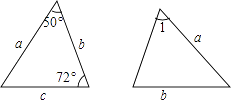
A、50° B、58° C、60° D、72°6. 点P（2，﹣3）关于x轴的对称点是（ ）A、（﹣2，3） B、（2，3） C、（﹣2，-3） D、（2，﹣3）7. 一个多边形的内角和是外角和的2倍，则这个多边形是（）A、四边形 B、五边形 C、六边形 D、八边形8. 下列长度的三条线段，不能组成三角形的是（ ）A、2、3、4 B、1、2、3 C、3、4、5 D、4、5、69. 如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠1=35°，则∠2等于（ ）
A、35° B、45° C、55° D、65°10. 如图，已知BE，CF分别为△ABC的两条高，BE和CF相交于点H，若∠BAC=50°，则∠BHC为（ ）
A、115° B、120° C、125° D、130°11. 如图，AD是△ABC中∠BAC的平分线，DE⊥AB于点E，DF⊥AC交AC于点F．S△ABC=7，DE=2，AB=4，则AC长是（ ）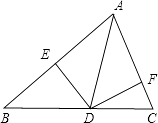
A、4 B、3 C、6 D、512. 已知等腰三角形的一个内角为50°，则这个等腰三角形的顶角为（ ）A、50° B、80° C、50°或80° D、40°或65°13. 小强站在镜前，从镜子中看到镜子对面墙上挂着的电子表，其读数如图所示，则电子表的实际时刻是（ ）
A、15：01 B、10：51 C、10：21 D、12：0114.如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，当∠EPF在△ABC内绕顶点P旋转时（点E不与A、B重合），给出以下四个结论：①AE=CF；②△EPF是等腰直角三角形；③2S四边形AEPF=S△ABC；④BE+CF=EF．上述结论中始终正确的有（ ）
A、4个 B、3个 C、2个 D、1个二、解答题
-
15. 已知：如图，M是AB的中点，∠1=∠2，MC=MD．求证：∠A=∠B．
16. 如图，等边△ABC的周长是9，
(1)、求作AC的中点D；（保留作图痕迹）(2)、E在BC的延长线上．若DE=DB，求CE的长．17. 如图，已知△ABC的三个顶点在格点上．
(1)、作出与△ABC关于x轴对称的图形△A1B1C1；(2)、求出A1 ， B1 ， C1三点坐标；(3)、求△ABC的面积．18. 如图，E、F分别是等边三角形ABC的边AB、AC上的点，且BE=AF，CE与BF交于点P．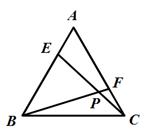
(1)、求证：CE=BF；(2)、求∠BPC的度数．19. 如图，∠AOB=30度，OC平分∠AOB，P为OC上一点，PD∥OA交OB于D，PE垂直OA于E，若OD=4cm，求PE的长．
20. 已知，如图在坐标平面内，OA⊥OC，OA=OC，A（ ，1），求C点坐标
21. 如图，△ABC中，∠BAC=110°，DE、FG分别为AB、AC的垂直平分线，E、G分别为垂足．
(1)、求∠DAF的度数；(2)、如果BC=10cm，求△DAF的周长．22. 如图在等腰三角形△ABC中，AC=BC，D、E分别为AB、BC上一点，∠CDE=∠A．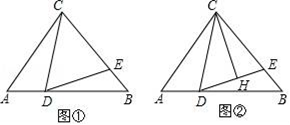
(1)、如图①，若BC=BD，求证：CD=DE；(2)、如图②，过点C作CH⊥DE，垂足为H，若CD=BD，EH=1，求DE﹣BE的值．23. 如图，在△ABC中，∠BAC=90°，AB=AC，D是AC边上一动点，CE⊥BD于E．
(1)、如图（1），若BD平分∠ABC时，①求∠ECD的度数；②延长CE交BA的延长线于点F，补全图形，探究BD与EC的数量关系，并证明你的结论；(2)、如图（2），过点A作AF⊥BE于点F，猜想线段BE，CE，AF之间的数量关系，并证明你的猜想．