湖北省安陆市2017-2018学年八年级上学期数学期中考试试卷
试卷更新日期:2019-01-24 类型:期中考试
一、单选题
-
1. 下面四个手机应用图标中是轴对称图形的是( )
 A、(A) B、(B) C、(C) D、(D)2. 已知图中的两个三角形全等,则 的大小为( )
A、(A) B、(B) C、(C) D、(D)2. 已知图中的两个三角形全等,则 的大小为( ) A、
A、 B、
C、
B、
C、 D、
D、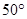 3. 如图,三角形被木板遮住一部分,这个三角形是( )
3. 如图,三角形被木板遮住一部分,这个三角形是( ) A、锐角三角形 B、直角三角形 C、钝角三角形 D、以上都有可能4.
A、锐角三角形 B、直角三角形 C、钝角三角形 D、以上都有可能4.如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( )
 A、图中有三个直角三角形 B、∠1=∠2 C、∠1和∠B都是∠A的余角 D、∠2=∠A5. 已知n边形从一个顶点出发可以作9条对角线,则n=( )A、9 B、10 C、11 D、126. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( )
A、图中有三个直角三角形 B、∠1=∠2 C、∠1和∠B都是∠A的余角 D、∠2=∠A5. 已知n边形从一个顶点出发可以作9条对角线,则n=( )A、9 B、10 C、11 D、126. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( ) A、1个 B、2个 C、3个 D、4个7. 如图,点O在△ABC内,且到三边的距离相等,若∠A=60 ,则∠BOC的大小为( )
A、1个 B、2个 C、3个 D、4个7. 如图,点O在△ABC内,且到三边的距离相等,若∠A=60 ,则∠BOC的大小为( ) A、
A、 B、
B、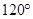 C、
C、 D、 60
D、 60  8. 如图,在Rt△ABC中,∠BAC=90 ,AD⊥BC于D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=( )
8. 如图,在Rt△ABC中,∠BAC=90 ,AD⊥BC于D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=( ) A、 30
A、 30 B、
C、 60
B、
C、 60  D、 75
D、 75  9. 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,……,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
9. 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,……,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )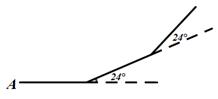 A、140米 B、150米 C、160米 D、240米10. 如图,在Rt△ABC中,∠ACB=90 ,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED= ;② ;③∠ADF= ;④CE=DF.正确的是( )
A、140米 B、150米 C、160米 D、240米10. 如图,在Rt△ABC中,∠ACB=90 ,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED= ;② ;③∠ADF= ;④CE=DF.正确的是( ) A、①②④ B、②③④ C、①③ D、①②③④
A、①②④ B、②③④ C、①③ D、①②③④二、填空题
-
11. 三角形三边长分别为3, ,7,则 的取值范围是 .12. 一个正多边形的内角和为540 ,则这个正多边形的每个外角的度数为 .13. 如图,已知AB⊥BD,AB∥DE,AB=ED。要说明△ABC≌△EDC,若添加AC=EC可用 公理(或定理)判定全等.
 14. 如图△ABC中,AD⊥BC,AE平分∠BAC,∠B=60 ,∠BAC=84 ,则∠DAE= .
14. 如图△ABC中,AD⊥BC,AE平分∠BAC,∠B=60 ,∠BAC=84 ,则∠DAE= . 15. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= ° .
15. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= ° . 16. 如图,已知△ABC的周长是21,BO,CO平分∠ABC,∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积 .
16. 如图,已知△ABC的周长是21,BO,CO平分∠ABC,∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积 . 17.
17.如图,在3×3的正方形网格中,已有两个小正方形被涂黑.再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的方法有 种.
 18. 如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为cm.
18. 如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为cm.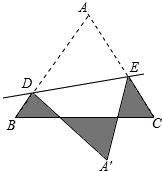 19. 在△ABC中,AC=BC,∠ACB=90 ,CE是过C点的一条直线,AD⊥CE于D,BE⊥CE于E,若DE=6,AD=3,则BE= .
19. 在△ABC中,AC=BC,∠ACB=90 ,CE是过C点的一条直线,AD⊥CE于D,BE⊥CE于E,若DE=6,AD=3,则BE= .三、解答题
-
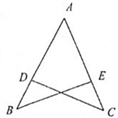
20. 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:BD=CE.
 21. 如图,已知A(1,2),B(3,1),C(4,3).
21. 如图,已知A(1,2),B(3,1),C(4,3).
①作△ABC关于y轴的对称图形△A1B1C1 , 写出点C关于y轴的对称点C1的坐标;
②作△ABC关于直线m(直线m上各点的纵坐标都为-1)的对称图形△A2B2C2 , 写出点C关于直线m的对称点C2的坐标.
22. 如图,已知∠1=∠2=∠3,且∠BAC=70 ,∠DFE=50 ,求∠ABC的度数. 23. 在△ABC中,AB边的垂直平分线lḻ交BC于点D,AC边的垂直平分线l2交BC于点E,lḻ与 l2相交于点O,连接AD,AE, △ADE的周长为6cm .
23. 在△ABC中,AB边的垂直平分线lḻ交BC于点D,AC边的垂直平分线l2交BC于点E,lḻ与 l2相交于点O,连接AD,AE, △ADE的周长为6cm .
(1)、求BC的长;(2)、分别连接OA,OB,OC,若△OBC的周长为16cm,求OA的长.24. 如图,线段AC、BD交于点M,过B、D两点分别作AC的垂线段BF、DE, AB=CD (1)、若∠A=∠C,求证:FM=EM;(2)、若FM=EM,则∠A=∠C.是真命题吗?(直接判断,不必证明)(25. 如图a,在平面直角坐标系中,A、B坐标分别为(6,0),(0,6),P为线段AB上的一点.
(1)、若∠A=∠C,求证:FM=EM;(2)、若FM=EM,则∠A=∠C.是真命题吗?(直接判断,不必证明)(25. 如图a,在平面直角坐标系中,A、B坐标分别为(6,0),(0,6),P为线段AB上的一点. (1)、如图a,若三角形OAP的面积是12,求点P的坐标;(2)、如图b,若P为AB的中点,点M,N分别是OA,OB边上的动点,点M从顶点A,点N从顶点O同时出发,且它们的速度都为1cm/s,则在M,N运动的过程中,线段PM,PN之间有何关系?并证明;(3)、如图c,若P为线段AB上异于A,B的任意一点,过B点作BD⊥OP,交OP,OA分别于F,D两点,E为OA上一点,且∠PEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.
(1)、如图a,若三角形OAP的面积是12,求点P的坐标;(2)、如图b,若P为AB的中点,点M,N分别是OA,OB边上的动点,点M从顶点A,点N从顶点O同时出发,且它们的速度都为1cm/s,则在M,N运动的过程中,线段PM,PN之间有何关系?并证明;(3)、如图c,若P为线段AB上异于A,B的任意一点,过B点作BD⊥OP,交OP,OA分别于F,D两点,E为OA上一点,且∠PEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.