湖北省襄阳市襄州区2017-2018学年七年级上学期数学期末考试试卷
试卷更新日期：2019-01-24 类型：期末考试
一、单选题
-
1. 下列美丽的图案中是轴对称图形的个数有（ ）
A、1个 B、2个 C、3个 D、4个2. 下列物品不是利用三角形稳定性的是（ ）A、自行车的三角形车架 B、三角形房架 C、照相机的三脚架 D、放缩尺3. 到三角形三条边的距离都相等的点是这个三角形的（ ）A、三条中线的交点 B、三条高的交点 C、三条边的垂直平分线的交点 D、三条角平分线的交点4. 如图，点A ， D ， C ， E在同一条直线上，AB∥EF ， AB＝EF ， ∠B＝∠F ， AE＝10，AC＝7，则CD的长为（ ）
A、5.5 B、4 C、4.5 D、35. 已知点A的坐标为（﹣2，3），点B与点A关于x轴对称，点C与点B关于y轴对称，则点C关于x轴对称的点的坐标为（ ）A、（2，﹣3） B、（﹣2，3） C、（2，3） D、（﹣2，﹣3）6. 如果把分式中的x和y都扩大2倍，则分式的值（ ）A、扩大4倍 B、扩大2倍 C、不变 D、缩小2倍7. 下列计算正确的是（ ）A、x4·x4=x16 B、（a3）2·a4=a9 C、（ab2）4÷（−ab）2=−ab4 D、 （a−1b3）2=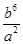
8. 若分式 的值为零，则x的值是（ ）A、1 B、﹣1 C、±1 D、29. 若分式 ，则分式 的值等于（ ）A、
；
B、
；
C、
；
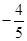D、
.
10. 如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下五个结论：
①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP； ⑤∠AOB=60°．
其中正确的结论的个数是（ ）
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 在△ABC中，∠A=60°，∠B=40°，则∠C的度数是 ．12. 若x2+mx+n分解因式的结果是（x+2）（x﹣1），则m+n的值为 ．13. a+b=2，ab=﹣2，则a2+b2= ．14. 若2m=a，32n=b，m，n为正整数，则23m+10n= ．15. 如图，∠AOB=30°，∠AOB内有一定点P，且OP=12，在OA上有一点Q，OB上有一点R，若△PQR周长最小，则最小周长是
16. 在等腰△ABC中，AB=AC，一边上的中线BD 将这个三角形的周长分为15和12两个部分，则该等腰三角形的底边长为 ．三、解答题
-
17. 分解因式：(1)、81x4﹣16(2)、8ab3+2a3b﹣8a2b218. 化简求值：（x﹣y+ ）（x+y﹣ ），其中x=97，y=3．19. 解方程：(1)、 =(2)、 ﹣ =20. 在创建文明城市的进程中，我市为美化城市环境，计划种值树木60万棵，由于志愿者的加入，实际每天植树比原计划多20%，结果提前5天完成任务，求原计划每天植树多少万棵？21. 如图，在△ABC中，BD平分∠ABC，
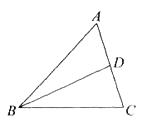(1)、作图：作BC边的垂直平分线分别交BC，BD于点E，F（用尺规作图法，保留作图痕迹，不要求写作法）；
(2)、在（1）的条件下，连接CF，若∠A=60°，∠ABD=24°，求∠ACF的度数.22. 如图，BD是△ABC的角平分线，DE⊥AB，DF⊥BC垂足分别为E、F．
(1)、求证：BE=BF；(2)、若△ABC的面积为70，AB=16，DE=5，则BC= ．23. 如图1，在四边形ABCD中，DC∥AB，AD=BC，BD平分∠ABC．
(1)、求证：AD=DC；(2)、如图2，在上述条件下，若∠A=∠ABC=60°，过点D作DE⊥AB，过点C作CF⊥BD，垂足分别为E、F，连接EF．判断△DEF的形状并证明你的结论．24. 在Rt△ABC中，∠ACB=90°，AC=BC，CD是∠ACB的角平分线，点E，F分别是边AC， BC上的动点，AC=4，设AE=x，BF=y．
(1)、若x+y=3，求四边形CEDF的面积；(2)、当DE⊥DF时，如图2，试探索x、y之间的数量关系．25. 如图1所示，在Rt△ABC中，∠C=90°，点D是线段CA延长线上一点，且AD=AB．点F是线段AB上一点，连接DF，以DF为斜边作等腰Rt△DFE，连接EA，EA满足条件EA⊥AB．
(1)、若∠AEF=20°，∠ADE=50°，AC=2，求AB的长度；(2)、求证：AE=AF+BC；(3)、如图2，点F是线段BA延长线上一点，探究AE、AF、BC之间的数量关系，并证明．