湖北省恩施州利川市2017-2018学年七年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、单选题
-
1. 计算(﹣x2)3的结果是( )A、﹣x6 B、x6 C、﹣x5 D、﹣x82. 四边形的内角和为( )A、180° B、360° C、540° D、720°3. 下列图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、﹣a×(﹣a)2=a3 B、a×(﹣a)3=a4 C、 a6÷(2a)2= a3 D、 a6÷(2a)2= a45. 若等腰三角形的底角是顶角的2倍,则这个等腰三角形的底角的度数是( )A、36° B、72° C、36°或72° D、无法确定的6. 若分式 有意义,则a满足的条件是( )A、a≠1的实数 B、a为任意实数 C、a≠1或﹣1的实数 D、a=﹣17. 下列各式中的最简分式是( )A、
4. 下列运算正确的是( )A、﹣a×(﹣a)2=a3 B、a×(﹣a)3=a4 C、 a6÷(2a)2= a3 D、 a6÷(2a)2= a45. 若等腰三角形的底角是顶角的2倍,则这个等腰三角形的底角的度数是( )A、36° B、72° C、36°或72° D、无法确定的6. 若分式 有意义,则a满足的条件是( )A、a≠1的实数 B、a为任意实数 C、a≠1或﹣1的实数 D、a=﹣17. 下列各式中的最简分式是( )A、 B、
B、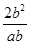 C、
C、 D、
D、 8. 分解因式x4-1的结果是( )A、(x+1)(x-1) B、(x2+1)(x2-1) C、(x2+1)(x+1)(x-1) D、(x+1)2(x-1)29. 如图,在等边△ABC中,AD是BC边上的高,∠BDE=∠CDF=30°,在下列结论中:①△ABD≌△ACD;②2DE=2DF=AD;③△ADE≌△ADF;④4BE=4CF=AB.正确的个数是( )
8. 分解因式x4-1的结果是( )A、(x+1)(x-1) B、(x2+1)(x2-1) C、(x2+1)(x+1)(x-1) D、(x+1)2(x-1)29. 如图,在等边△ABC中,AD是BC边上的高,∠BDE=∠CDF=30°,在下列结论中:①△ABD≌△ACD;②2DE=2DF=AD;③△ADE≌△ADF;④4BE=4CF=AB.正确的个数是( ) A、1 B、2 C、3 D、410. 如图,将两块相同的三角板(含30°角)按图中所示位置摆放,若BE交CF于D,AC交BE于M,AB交CF于N,则下列结论中错误的是( )
A、1 B、2 C、3 D、410. 如图,将两块相同的三角板(含30°角)按图中所示位置摆放,若BE交CF于D,AC交BE于M,AB交CF于N,则下列结论中错误的是( )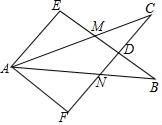 A、∠EAC=∠FAB B、∠EAF=∠EDF C、△ACN≌△ABM D、AM=AN11. A、B两地相距48km,一艘轮船从A地顺流航行至B地,比从B地逆流航行至A地少用2h,已知水流速度为5km/h,求该轮船在静水中的航行速度是多少km/h?若设该轮船在静水中的速度为xkm/h,则可列方程( )A、
A、∠EAC=∠FAB B、∠EAF=∠EDF C、△ACN≌△ABM D、AM=AN11. A、B两地相距48km,一艘轮船从A地顺流航行至B地,比从B地逆流航行至A地少用2h,已知水流速度为5km/h,求该轮船在静水中的航行速度是多少km/h?若设该轮船在静水中的速度为xkm/h,则可列方程( )A、 =2
B、
=2
B、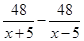 =2
C、
=2
C、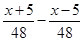 =2
D、
=2
D、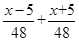 =2
=2
二、填空题
-
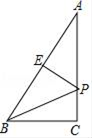
12. 分解因式:2a3+8a2b+8ab2= .13. 若分式 的值为零,则m,n满足的条件是 .14. 一个等腰三角形的边长分别是4cm和7cm,则它的周长是15. 如图,在Rt△ABC中,∠A=30°,∠C=90°,E是斜边AB的中点,点P为AC边上一动点,若Rt△ABC的直角边AC=4,则PB+PE的最小值等于 .
三、解答题
-
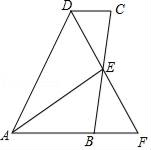
16. 计算(a﹣3b)(a+3b)﹣(﹣a﹣2b)(a﹣2b)17. 解方程:18. 先化简,再求值:(1﹣ )÷ ,其中x=19. 计算( )2• ﹣20. 如图,AB∥CD,E是BC的中点,DE平分∠ADC,DE的延长线交AB于点F,求证:AE平分∠DAF
 21. 等腰三角形两腰上的中线相等吗?试证明你的结论22. 从甲地到乙地有120千米,一辆小车与一辆卡车同时从甲地出发,沿相同路线开往乙地,已知小车的速度是卡车的1.5倍,结果小车比卡车提前30分钟到达乙地.求小车和卡车的行驶速度各是多少?23. 如图①,在△ABC中,AB=AC,点P为边BC上异于B和C的任意一点,过点P作PD⊥AB于D,作PE⊥AC于E,过点C作CF⊥AB于F,求证:PD+PE=CF.
21. 等腰三角形两腰上的中线相等吗?试证明你的结论22. 从甲地到乙地有120千米,一辆小车与一辆卡车同时从甲地出发,沿相同路线开往乙地,已知小车的速度是卡车的1.5倍,结果小车比卡车提前30分钟到达乙地.求小车和卡车的行驶速度各是多少?23. 如图①,在△ABC中,AB=AC,点P为边BC上异于B和C的任意一点,过点P作PD⊥AB于D,作PE⊥AC于E,过点C作CF⊥AB于F,求证:PD+PE=CF.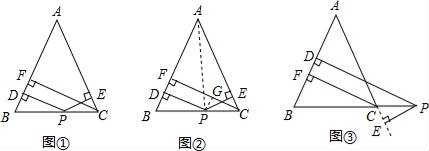 (1)、有下面两种证明思路:(一)如图②,连接AP,由△ABP于△ACP面积之和等于△ABC的面积证得PD+PE=CF.(二)如图②,过点P作PG⊥CF,垂足为G,可以证明:PD=GF,PE=CG,则PD+PE=CF.
(1)、有下面两种证明思路:(一)如图②,连接AP,由△ABP于△ACP面积之和等于△ABC的面积证得PD+PE=CF.(二)如图②,过点P作PG⊥CF,垂足为G,可以证明:PD=GF,PE=CG,则PD+PE=CF.请你选择其中的一种证明思路完成证明:
(2)、探究:如图③,当点P在BC的延长线上时,其它条件不变,探究并证明PD、PE和CF间的数量关系;(3)、猜想:当点P在CB的延长线上时,其它条件不变,猜想PD、PE和CF间的数量关系(不要求证明)