湖北省大冶市2017-2018学年七年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、单选题
-
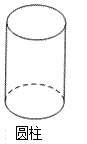
1. 如果水位升高 米记为 米,那么水位下降 米应记为( )A、-1米 B、+1米 C、-2米 D、+2米2. 下列运算中,结果正确的是( )A、6xy﹣4xy=2xy B、3x2+2=5x2 C、4x+3y=7xy D、5x2﹣x2=43. 下列方程中,解为x=2的方程是( )A、x﹣1=4 B、3x=1﹣x C、2(x﹣1)=1 D、4x﹣1=2x+34. 下列基本几何体中,从正面、上面、左面观察都是相同图形的是( )A、
 B、
B、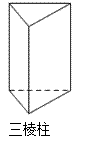 C、
C、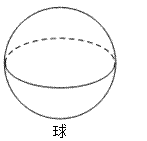 D、
D、 5. 下列各组单项式中,是同类项的一组是( )A、3x2y与3xy2 B、2abc与﹣3ac C、﹣2xy与yx D、2xy与2ab6. A、B两地的位置如图所示,则A在B的( )
5. 下列各组单项式中,是同类项的一组是( )A、3x2y与3xy2 B、2abc与﹣3ac C、﹣2xy与yx D、2xy与2ab6. A、B两地的位置如图所示,则A在B的( ) A、南偏东30° B、东偏南60° C、西偏北30° D、北偏西60°7. 已知a+2b=3,则代数式2a+4b+1的值为( )A、5 B、6 C、7 D、88. 有理数a、b在数轴上的对应的位置如图所示,则( )
A、南偏东30° B、东偏南60° C、西偏北30° D、北偏西60°7. 已知a+2b=3,则代数式2a+4b+1的值为( )A、5 B、6 C、7 D、88. 有理数a、b在数轴上的对应的位置如图所示,则( )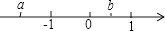 A、a+b<0 B、a+b>0 C、a﹣b=0 D、a﹣b>09. 某车间原计划13小时生产一批零件,后来每小时多生产10件,用了12小时不但完成任务,而且还多生产60件,设原计划每小时生产x个零件,则所列方程为( )A、13x=12(x+10)+60 B、12(x+10)=13x+60 C、
A、a+b<0 B、a+b>0 C、a﹣b=0 D、a﹣b>09. 某车间原计划13小时生产一批零件,后来每小时多生产10件,用了12小时不但完成任务,而且还多生产60件,设原计划每小时生产x个零件,则所列方程为( )A、13x=12(x+10)+60 B、12(x+10)=13x+60 C、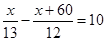 D、
D、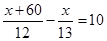 10. 如果线段AB=13cm,MA+MB=17 cm,那么下面说法中正确的是( ).A、M点在线段AB上 B、M点在直线AB上 C、M点在直线AB外 D、M点可能在直线AB上,也可能在直线AB外
10. 如果线段AB=13cm,MA+MB=17 cm,那么下面说法中正确的是( ).A、M点在线段AB上 B、M点在直线AB上 C、M点在直线AB外 D、M点可能在直线AB上,也可能在直线AB外二、填空题
-
11. 1cm2 的手机上约有细菌 120 000 个,120 000 用科学记数法表示为 .12. 56.28°=°′″.13. 定义a*b=ab+a+b,若3*x=27,则x的值是。14. 如图,点C在线段AB上,D是线段AC的中点,若CB=2,CD=3CB,则线段AB的长 .
 15. 某书店把一本新书按标价的九折出售,仍可获利 20%.若该书的进价为 21 元,则标价为元.16. 中午12点30分时,钟面上时针和分针的夹角是度.17. 如图长方形MNPQ是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,中间最小的正方形A的边长是1,观察图形特点可知长方形相对的两边是相等的(如图中MN=PQ).正方形四边相等.请根据这个等量关系,试计算长方形MNPQ的面积,结果为 .
15. 某书店把一本新书按标价的九折出售,仍可获利 20%.若该书的进价为 21 元,则标价为元.16. 中午12点30分时,钟面上时针和分针的夹角是度.17. 如图长方形MNPQ是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,中间最小的正方形A的边长是1,观察图形特点可知长方形相对的两边是相等的(如图中MN=PQ).正方形四边相等.请根据这个等量关系,试计算长方形MNPQ的面积,结果为 .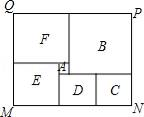
三、解答题
-
18. 计算:(1)、13+(﹣7)﹣(﹣9)+5×(﹣2);(2)、|﹣3 |× ÷ ÷(﹣3)2 .19. 先化简,再求值:3x2y﹣[6xy﹣4( xy﹣ x2y)],其中x=﹣1,y=2018.20. 解下列方程:(1)、8x﹣7=2x+11;(2)、 .21. 把若干块糖分给小朋友,若每人3块,则多12块;若每人5块,则缺10块,问一共有多少个小朋友?22. 如图,已知∠AOB=155°,∠AOC=∠BOD=90°.
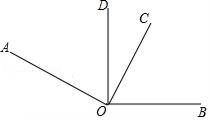 (1)、写出与∠COD互余的角;(2)、求∠COD的度数;(3)、图中是否有互补的角?若有,请写出来.23. 某租赁公司拥有100辆轿车,当每辆轿车的月租金为3000元时,可全部租出,当每辆轿车的月租金每增加50元时,未租出的轿车将会增加一辆,租出的轿车每辆每月公司需要保养费150元,未租出的轿车每辆每月公司需要保养费50元.(1)、已知10月份每辆轿车的月租金为3600元,该月租出多少辆轿车?(2)、已知11月份的保养费总开支为12900元,问该月租出了多少辆轿车?24. 如图,O为直线AB上一点,∠BOC=α.
(1)、写出与∠COD互余的角;(2)、求∠COD的度数;(3)、图中是否有互补的角?若有,请写出来.23. 某租赁公司拥有100辆轿车,当每辆轿车的月租金为3000元时,可全部租出,当每辆轿车的月租金每增加50元时,未租出的轿车将会增加一辆,租出的轿车每辆每月公司需要保养费150元,未租出的轿车每辆每月公司需要保养费50元.(1)、已知10月份每辆轿车的月租金为3600元,该月租出多少辆轿车?(2)、已知11月份的保养费总开支为12900元,问该月租出了多少辆轿车?24. 如图,O为直线AB上一点,∠BOC=α.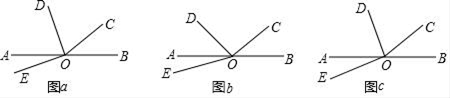 (1)、若α=40°,OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数;(2)、若∠AOD= ∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;(3)、若∠AOD= ∠AOC,∠DOE= (n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).25. A,B两点在数轴上的位置如图所示,其中O为原点,点A对应的有理数为﹣4,点B对应的有理数为6.
(1)、若α=40°,OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数;(2)、若∠AOD= ∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;(3)、若∠AOD= ∠AOC,∠DOE= (n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).25. A,B两点在数轴上的位置如图所示,其中O为原点,点A对应的有理数为﹣4,点B对应的有理数为6. (1)、动点P从点A出发,以每秒2个单位长度的速度向右运动,设运动时间为t秒(t>0).
(1)、动点P从点A出发,以每秒2个单位长度的速度向右运动,设运动时间为t秒(t>0).①当t=1时,AP的长为 ,点P表示的有理数为 ;
②当PB=2时,求t的值;(2)、如果动点P以每秒6个单位长度的速度从O点向右运动,点A和B分别以每秒1个单位长度和每秒3个单位长度的速度向右运动,且三点同时出发,那么经过几秒PA=2PB.