河南省南阳市南召县2017-2018学年七年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、单选题
-
1. ﹣5的绝对值是( )A、5 B、 C、 ﹣ D、﹣52. 下列叙述不正确的是( )A、两点之间,线段最短 B、对顶角相等 C、 单项式﹣
 的次数是5
D、等角的补角相等
3. 下列各组中,不是同类项的是( )A、52与25 B、﹣ab与ba C、 0.2a2b与﹣ a2b D、a2b3与﹣a3b24. 如图所示,数轴上A、B两点分别对应有理数a,b,则下列结论中正确的是( )
的次数是5
D、等角的补角相等
3. 下列各组中,不是同类项的是( )A、52与25 B、﹣ab与ba C、 0.2a2b与﹣ a2b D、a2b3与﹣a3b24. 如图所示,数轴上A、B两点分别对应有理数a,b,则下列结论中正确的是( ) A、a+b>0 B、ab>0 C、|a|﹣|b|>0 D、a﹣b>05. 若点C在线段AB上,则下列条件中不能确定点C是线段AB中点的是( )A、AC=BC B、AC+BC=AB C、AB=2AC D、 BC= AB6. 下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A、a+b>0 B、ab>0 C、|a|﹣|b|>0 D、a﹣b>05. 若点C在线段AB上,则下列条件中不能确定点C是线段AB中点的是( )A、AC=BC B、AC+BC=AB C、AB=2AC D、 BC= AB6. 下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A、 B、
B、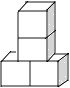 C、
C、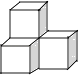 D、
D、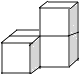 7. 如图,已知∠1=70°,要使AB∥CD,则须具备另一个条件( )
7. 如图,已知∠1=70°,要使AB∥CD,则须具备另一个条件( ) A、∠2=70° B、∠2=100° C、∠2=110° D、∠3=110°8. 已知a﹣b=3,c+d=2,则(b+c)﹣(a﹣d)的值是( )A、15 B、1 C、﹣5 D、﹣19. 若M=4x2-5x+11,N=3x2-5x+10,则M和N的大小关系是( )
A、∠2=70° B、∠2=100° C、∠2=110° D、∠3=110°8. 已知a﹣b=3,c+d=2,则(b+c)﹣(a﹣d)的值是( )A、15 B、1 C、﹣5 D、﹣19. 若M=4x2-5x+11,N=3x2-5x+10,则M和N的大小关系是( )
A、M>N B、M=N C、M<N D、无法确定10. 已知a是两位数,b是一位数,把a接写在b的后面,就成为一个三位数.这个三位数可表示成( )A、10b+a B、ba C、100b+a D、b+10a二、填空题
-
11. a的相反数是 .12. ∠α=50°17′,∠α的余角的大小为 .13. 若﹣ a2bm与4anb是同类项,则m﹣n= .14. 如图,把这个平面展开图折叠成立方体,与“祝”字相对的字是 .
 15. 如图,B、A、E三点在同一直线上,请你添加一个条件,使AD∥BC.你所添加的条件是(不允许添加任何辅助线).
15. 如图,B、A、E三点在同一直线上,请你添加一个条件,使AD∥BC.你所添加的条件是(不允许添加任何辅助线).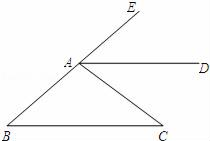
三、解答题
-
16. 计算:﹣14﹣ ×[5﹣(﹣3)2].17. ( ﹣ + )÷(﹣ )18. 先化简,再求值:(3x2y+5x)﹣[x2y﹣4(x﹣x2y)],其中(x+2)2+|y﹣3|=0.19. 操作:如图,直线AB与CD交于点O,按要求完成下列问题.
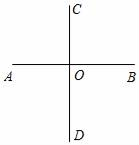 (1)、用量角器量得∠AOC=度.AB与CD的关系可记作 .(2)、画出∠BOC的角平分线OM,∠BOM=∠=度.(3)、①在射线OM上取一点P,画出点P到直线AB的距离PE.
(1)、用量角器量得∠AOC=度.AB与CD的关系可记作 .(2)、画出∠BOC的角平分线OM,∠BOM=∠=度.(3)、①在射线OM上取一点P,画出点P到直线AB的距离PE.②如图若按“上北下南左西右东”的方位标记,请画出表示“南偏西30°”的射线OF.
20. 如图,点C为线段AB上一点,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点. (1)、求线段MN的长;(2)、若AC+BC=acm,其他条件不变,直接写出线段MN的长为 .21. 根据解答过程填空(理由或数学式)
(1)、求线段MN的长;(2)、若AC+BC=acm,其他条件不变,直接写出线段MN的长为 .21. 根据解答过程填空(理由或数学式)如图,已知∠1=∠2,∠D=60°,求∠B的度数.

解∵∠2=∠3()
又∵∠1=∠2(已知),
∴∠3=∠1(等量代换)
∴∥()
∴∠D+∠B=180°()
又∵∠D=60°(已知),
∴∠B= .
22. 某商场购进一批西服,进价为每套250元,原定每套以390元的价格销售,这样每天可销售50套.如果每套比原销售价降低10元销售,则每天可多销售5套.该商场为了确定销售价格,作了如下测算,请你参加测算,并由此归纳得出结论(每套西服的利润=每套西服的销售价﹣每套西服的进价)(1)、①按原销售价销售,每天可获利润元;②若每套降低10元销售,每天可获利润元;
(2)、如果每套销售价降低10元,每天就多销售5套,每套销售价降低20元,每天就多销售10套,每套销售价降低30元,每天就多销售15套…按这种方式:
①若每套降低10a元,则每套的销售价格为元;(用代数式表示)
②若每套降低10a元,则每天可销售套西服:(用代数式表示)
③若每套降低10a元,则每天共可以获利润元.(用代数式表示)
23. 阅读理解
如图1,已知点A是BC外一点,连接AB,AC,求∠BAC+∠B+∠C的度数.
(1)、阅读并补充下面推理过程解:过点A作ED∥BC
∴∠B=∠ , ∠C=∠ .
又∵∠EAB+∠BAC+∠DAC=180°(平角定义)
∴∠B+∠BAC+∠C=180°
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决
(2)、如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.小明受到启发,过点C作CF∥AB如图所示,请你帮助小明完成解答:
(3)、已知AB∥CD,点C在点D的右侧,∠ADC=70°.BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.①如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为°.
②如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为°(用含n的代数式表示)