湖北省孝感市2018届九年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、单选题
-
1. 下列四种标志图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程 的根的情况是( )A、两个实根和为5 B、两个实根之积为7 C、有两个相等的实数根 D、没有实数根3. 在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )A、12 B、9 C、4 D、34. 将抛物线 向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为( )A、
2. 一元二次方程 的根的情况是( )A、两个实根和为5 B、两个实根之积为7 C、有两个相等的实数根 D、没有实数根3. 在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )A、12 B、9 C、4 D、34. 将抛物线 向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为( )A、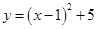 B、
B、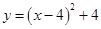 C、
C、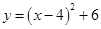 D、
D、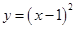 5. 如图,AB是⊙O的直径, ,∠COD=38°,则∠AEO的度数是( )
5. 如图,AB是⊙O的直径, ,∠COD=38°,则∠AEO的度数是( )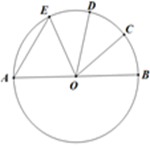 A、52° B、57° C、66° D、78°6. 如果一个矩形的宽(即短边)与长(即长边)之比是 ,那么这个矩形称为黄金矩形.如图,矩形ABCD是黄金矩形,点E,F,G,H分别为线段AD,BC,AB,EF的中点,则图中黄金矩形的个数是( )
A、52° B、57° C、66° D、78°6. 如果一个矩形的宽(即短边)与长(即长边)之比是 ,那么这个矩形称为黄金矩形.如图,矩形ABCD是黄金矩形,点E,F,G,H分别为线段AD,BC,AB,EF的中点,则图中黄金矩形的个数是( )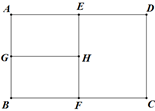 A、5个 B、4个 C、3个 D、2个7. 某商店今年10月份的销售额是3万元,12月份的销售额是6.75万元,从10月份到12月份,该店销售额平均每月的增长率是( )
A、5个 B、4个 C、3个 D、2个7. 某商店今年10月份的销售额是3万元,12月份的销售额是6.75万元,从10月份到12月份,该店销售额平均每月的增长率是( )
A、25% B、30% C、40% D、50%8. 在平面直角坐标系xOy中,将等腰直角三角形AOB按如图所示的位置放置,然后绕原点O逆时针旋转90°到△A'OB'的位置,若点B的坐标为B(4,0),则点A' 的坐标为( )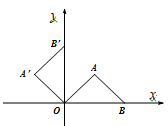 A、(2,2) B、 ( , ) C、(-2,2) D、 (- , )9. 关于 的方程 有两个不相等的实数根,则整数 的最大值是( )A、0 B、1 C、2 D、310. 如图,抛物线 的顶点为B(1,3),与 轴的交点A在点 (2,0)和(3,0)之间.以下结论:
A、(2,2) B、 ( , ) C、(-2,2) D、 (- , )9. 关于 的方程 有两个不相等的实数根,则整数 的最大值是( )A、0 B、1 C、2 D、310. 如图,抛物线 的顶点为B(1,3),与 轴的交点A在点 (2,0)和(3,0)之间.以下结论:① ;② ;③ ;④ ≥ ;⑤若 ,且 ,
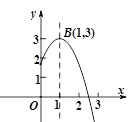
则 .其中正确的结论有( )
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 正六边形的边长为4,则它的外接圆半径是 .12. 从 ,0,π,3.1415,7这5个数中随机抽取一个数,抽到的数为有理数的概率是 .13. 如图,圆锥的侧面展开图是一个圆心角为120°的扇形,若圆锥的底面圆半径是 ,则圆锥的母线 的长= .
 14. 如图,点A在双曲线 (x>0)上,点B在双曲线 上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60° ,则 k= .
14. 如图,点A在双曲线 (x>0)上,点B在双曲线 上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60° ,则 k= .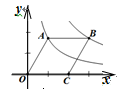 15. 如图,A、B、C、D四个点在同一个圆上,∠ADC=90°,AB=7cm,CD=5cm,AE=4cm,CF=6cm,则阴影部分的面积为cm2 .
15. 如图,A、B、C、D四个点在同一个圆上,∠ADC=90°,AB=7cm,CD=5cm,AE=4cm,CF=6cm,则阴影部分的面积为cm2 .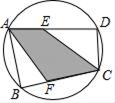 16. 如图,正△ABC的边长为4,将正△ABC绕点B顺时针旋转120°得到△C'A'B,若点D为直线A'B上的一动点,则AD+CD的最小值是 .
16. 如图,正△ABC的边长为4,将正△ABC绕点B顺时针旋转120°得到△C'A'B,若点D为直线A'B上的一动点,则AD+CD的最小值是 .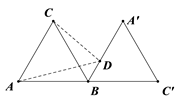
三、解答题
-
17. 用适当的方法解下列方程:(1)、(2)、18. 轿车经过孝感某高速收费站时,有三个收费通道A,B,C可随机选择其中一个通过.(1)、一辆轿车经过收费站时,选择A通道通过的概率是;(2)、若两辆轿车经过此收费站时,请你求出选择不同通道通过的概率.(用画树状图或列表法求解)19. 如图,在正方形ABCD中,E是AD边的中点.
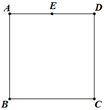 (1)、用直尺和圆规作⊙O,使⊙O 经过B、C、E三点;(要求:尺规作图,保留作图痕迹,不写作法);(2)、若正方形的边长为4,求(1)中所作⊙O的面积.20. 在平面直角坐标 中,已知三点A(1,3),B(3,3),C(3,1),反比例函数 的图象经过其中的两点,另外一点在直线 上.
(1)、用直尺和圆规作⊙O,使⊙O 经过B、C、E三点;(要求:尺规作图,保留作图痕迹,不写作法);(2)、若正方形的边长为4,求(1)中所作⊙O的面积.20. 在平面直角坐标 中,已知三点A(1,3),B(3,3),C(3,1),反比例函数 的图象经过其中的两点,另外一点在直线 上. (1)、填空: = , =;(2)、请你求出直线 与反比例函数 的图象的交点坐标;(3)、当 时,请直接写出相应的 的范围.21. 已知关于x的一元二次方程 有两个不相等的实数根 , .(1)、求 的取值范围;(2)、若 , 满足 ,且 为整数,求 的值.22. 2017年金卉庄园“新春祈福灯会”前夕,我市某工艺厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
(1)、填空: = , =;(2)、请你求出直线 与反比例函数 的图象的交点坐标;(3)、当 时,请直接写出相应的 的范围.21. 已知关于x的一元二次方程 有两个不相等的实数根 , .(1)、求 的取值范围;(2)、若 , 满足 ,且 为整数,求 的值.22. 2017年金卉庄园“新春祈福灯会”前夕,我市某工艺厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:销售单价 (元/件)
. ..
30
40
50
60
. ..
每天销售量 (件)
. ..
200
180
160
140
. ..
(1)、已知上表数据满足以下三个函数模型中的一个:① ;② ;③ 为常数, 中,请你求出 与 的函数关系式(不必写自变量的范围);(2)、求工艺厂试销该工艺品每天获得的利润 与 的函数关系式,并求当销售单价为多少时,每天获得的利润最大?最大利润是多少?(3)、孝感市物价部门规定,该工艺品销售单价最高不能超过72元/件,那么销售单价定为多少时,工艺厂试销工艺品每天获得的利润最大?23. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CP∥AB,在CP上截取CF=CD,连接BF. (1)、求证:直线BF是⊙O的切线;(2)、若AB=5,BC= ,求线段CD和BF的长.24. 抛物线 与 轴交于A(4,0),B(6,0)两点,与 轴交于点C(0,3).
(1)、求证:直线BF是⊙O的切线;(2)、若AB=5,BC= ,求线段CD和BF的长.24. 抛物线 与 轴交于A(4,0),B(6,0)两点,与 轴交于点C(0,3). (1)、求抛物线的解析式;(2)、点P从点O出发,以每秒2个单位长度的速度向点B运动,同时点E也从点O出发,以每秒1个单位长度的速度向点C运动,设点P的运动时间为t秒(0<t<3).
(1)、求抛物线的解析式;(2)、点P从点O出发,以每秒2个单位长度的速度向点B运动,同时点E也从点O出发,以每秒1个单位长度的速度向点C运动,设点P的运动时间为t秒(0<t<3).①过点E作x轴的平行线,与BC相交于点D(如图所示),当t为何值时,△PDE的面积最大,并求出这个最大值;
②当t =2时,抛物线的对称轴上是否存在点F,使△EFP为直角三角形?若存在,请你求出点F的坐标;若不存在,请说明理由.