湖北省襄阳老河口市2018届九年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、单选题
-
1. 一元二次方程x2﹣6x﹣5=0配方可变形为( )A、(x﹣3)2=14 B、(x﹣3)2=4 C、(x+3)2=14 D、(x+3)2=42. 若二次函数y=x2-mx+1的图象的顶点在x轴上,则m的值是( )A、2 B、-2 C、0 D、±23. 在下列四个图案中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 过⊙O内一点M的最长弦长为10cm,最短弦长为8cm,那么OM长为( )A、3cm B、6cm C、 cm D、9cm5. 气象台预报“本市明天降水概率是80%”,对此信息,下面的几种说法正确的是( )A、本市明天将有80%的地区降水 B、本市明天将有80%的时间降水 C、明天肯定下雨 D、明天降水的可能性比较大6. 如图,下列条件中不能判定△ACD∽△ABC的是( )
4. 过⊙O内一点M的最长弦长为10cm,最短弦长为8cm,那么OM长为( )A、3cm B、6cm C、 cm D、9cm5. 气象台预报“本市明天降水概率是80%”,对此信息,下面的几种说法正确的是( )A、本市明天将有80%的地区降水 B、本市明天将有80%的时间降水 C、明天肯定下雨 D、明天降水的可能性比较大6. 如图,下列条件中不能判定△ACD∽△ABC的是( ) A、
A、 B、∠ADC=∠ACB
C、∠ACD=∠B
D、AC2=AD·AB
7. 已知函数y= 的图象如图,当x≥﹣1时,y的取值范围是( )
B、∠ADC=∠ACB
C、∠ACD=∠B
D、AC2=AD·AB
7. 已知函数y= 的图象如图,当x≥﹣1时,y的取值范围是( )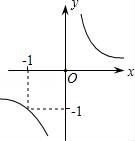 A、y<﹣1 B、y≤﹣1 C、y≤﹣1或y>0 D、y<﹣1或y≥08. 如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于sinA的是( )
A、y<﹣1 B、y≤﹣1 C、y≤﹣1或y>0 D、y<﹣1或y≥08. 如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于sinA的是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 在平面直角坐标系中,△ABC顶点A的坐标为(2,3).若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比为 ,则点A′的坐标为( )A、 (3,
9. 在平面直角坐标系中,△ABC顶点A的坐标为(2,3).若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比为 ,则点A′的坐标为( )A、 (3,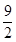 )
B、 (3,
)
B、 (3, 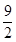 )或(-3,
)或(-3,  )
C、 (
)
C、 ( 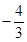 ,-2)
D、 ( ,2)或(
,-2)
D、 ( ,2)或( 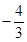 ,-2)
10. 如图,矩形OABC的面积为24,它的对角线OB与双曲线 相交于点D,且D为OB的中点,则k的值为( )
,-2)
10. 如图,矩形OABC的面积为24,它的对角线OB与双曲线 相交于点D,且D为OB的中点,则k的值为( )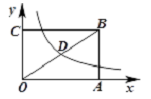 A、3 B、6 C、9 D、12
A、3 B、6 C、9 D、12二、填空题
-
11. 已知tanA= ,则锐角A的度数是 .12. 中午12点,身高为165cm的小冰直立时影长55cm,同学小雪此时在同一地点直立时影长为57cm,那么小雪的身高为cm.13. 二次函数y=(x﹣2m)2+1,当m<x<m+1时,y随x的增大而减小,则m的取值范围是 .14. 如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的正弦值是 .
 15. 如图,在矩形ABCD中,AB=4,BC=2.点E在边AB上,点F在边CD上,点G,H在对角线AC上.若四边形EGFH是菱形,则AE的长是 .
15. 如图,在矩形ABCD中,AB=4,BC=2.点E在边AB上,点F在边CD上,点G,H在对角线AC上.若四边形EGFH是菱形,则AE的长是 .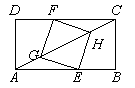 16. 如图,在Rt△ABC中,∠C=90°,∠BAC=60°,BC= ,将△ABC绕点A逆时针旋转60°后得到△ADE,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是(结果保留π).
16. 如图,在Rt△ABC中,∠C=90°,∠BAC=60°,BC= ,将△ABC绕点A逆时针旋转60°后得到△ADE,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是(结果保留π).
三、解答题
-
17. 在△ABC中,∠C=90°,AB=13,BC=5,求∠A的正弦值、余弦值和正切值.18. 如图,在△ABC中,正方形EDCF的三个顶点E,D,F都在三角形的边上,另一个顶点C与三角形的顶点重合,且AC=4,BC=6,求ED的长.
 19. 在一个不透明的布袋里装有三个标号分别为1,2,3的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,然后将小球放回布袋,小敏再从布袋中随机取出一个小球,记下数字为y,这样确定了点A的坐标为(x,y).请用列表或画树形图的方法,求点A在函数 图象上的概率.20. 如图,在某建筑物AB的顶部点A处观测,测得河对岸C处的俯角为30°,河的这一岸D处的俯角为60°,已知建筑物的高AB等于18米,求河宽CD.(结果保留根号)
19. 在一个不透明的布袋里装有三个标号分别为1,2,3的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,然后将小球放回布袋,小敏再从布袋中随机取出一个小球,记下数字为y,这样确定了点A的坐标为(x,y).请用列表或画树形图的方法,求点A在函数 图象上的概率.20. 如图,在某建筑物AB的顶部点A处观测,测得河对岸C处的俯角为30°,河的这一岸D处的俯角为60°,已知建筑物的高AB等于18米,求河宽CD.(结果保留根号) 21. 如图,直线y1=2x-3与双曲线 在第一象限交于点A,与x轴交于点B,过点A作AC⊥x轴,垂足为C,已知∠BAC=∠AOC.
21. 如图,直线y1=2x-3与双曲线 在第一象限交于点A,与x轴交于点B,过点A作AC⊥x轴,垂足为C,已知∠BAC=∠AOC. (1)、求A,B两点的坐标及k的值;(2)、请直接写出当y2>y1>0时x的取值范围.22. 如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线上的一点,过⊙O上一点C作⊙O的切线交DF于点E,CE⊥DF.
(1)、求A,B两点的坐标及k的值;(2)、请直接写出当y2>y1>0时x的取值范围.22. 如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线上的一点,过⊙O上一点C作⊙O的切线交DF于点E,CE⊥DF. (1)、求证:AC平分∠FAB;(2)、若AE=1,CE=2,求⊙O的半径.23. 一名男生推铅球,铅球行进的高度y(单位:m)与水平距离x(单位:m)之间的关系是 .(1)、铅球行进的最大高度是多少?(2)、该男生把铅球推出的水平距离是多少?(3)、铅球在下落的过程中,行进高度由 m变为 m时,铅球行进的水平距离是多少?24. 如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
(1)、求证:AC平分∠FAB;(2)、若AE=1,CE=2,求⊙O的半径.23. 一名男生推铅球,铅球行进的高度y(单位:m)与水平距离x(单位:m)之间的关系是 .(1)、铅球行进的最大高度是多少?(2)、该男生把铅球推出的水平距离是多少?(3)、铅球在下落的过程中,行进高度由 m变为 m时,铅球行进的水平距离是多少?24. 如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.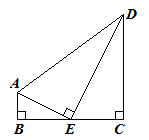 (1)、求证:△ABE∽△ECD;(2)、求证:AE2=AB·AD;(3)、若AB=1,CD=4,求线段AD,DE的长.25. 如图,□ABCD的两个顶点B,D都在抛物线y= x2+bx+c上,且OB=OC,AB=5,tan∠ACB= .
(1)、求证:△ABE∽△ECD;(2)、求证:AE2=AB·AD;(3)、若AB=1,CD=4,求线段AD,DE的长.25. 如图,□ABCD的两个顶点B,D都在抛物线y= x2+bx+c上,且OB=OC,AB=5,tan∠ACB= . (1)、求抛物线的解析式;(2)、在抛物线上是否存在点E,使以A,C,D,E为顶点的四边形是菱形?若存在,请求出点E的坐标;若不存在,请说明理由.(3)、动点P从点A出发向点D运动,同时动点Q从点C出发向点A运动,运动速度都是每秒1个单位长度,当一个点到达终点时另一个点也停止运动,运动时间为t(秒).当t为何值时,△APQ是直角三角形?
(1)、求抛物线的解析式;(2)、在抛物线上是否存在点E,使以A,C,D,E为顶点的四边形是菱形?若存在,请求出点E的坐标;若不存在,请说明理由.(3)、动点P从点A出发向点D运动,同时动点Q从点C出发向点A运动,运动速度都是每秒1个单位长度,当一个点到达终点时另一个点也停止运动,运动时间为t(秒).当t为何值时,△APQ是直角三角形?