湖北省武汉市2018届九年级上学期数学期末考试试卷

试卷更新日期：2019-01-24 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 方程x（x﹣5）＝0化成一般形式后，它的常数项是（   ）
    A、﹣5 B、5 C、0 D、1

    查看试题解析

  • 2. 二次函数y＝2（x﹣3）2﹣6（   ）
    A、最小值为﹣6 B、最大值为﹣6 C、最小值为3 D、最大值为3

    查看试题解析

  • 3. 下列交通标志中是中心对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 4. 事件①：射击运动员射击一次，命中靶心；事件②：购买一张彩票，没中奖，则（ ）
    A、事件①是必然事件，事件②是随机事件 B、事件①是随机事件，事件②是必然事件 C、事件①和②都是随机事件 D、事件①和②都是必然事件

    查看试题解析

  • 5. 抛掷一枚质地均匀的硬币，正面朝上的概率为0.5，下列说法正确的是（   ）
    A、连续抛掷2次必有1次正面朝上 B、连续抛掷10次不可能都正面朝上 C、大量反复抛掷每100次出现正面朝上50次 D、通过抛掷硬币确定谁先发球的比赛规则是公平的

    查看试题解析

  • 6. 一元二次方程x2＋2 3 x＋m＝0有两个不相等的实数根，则（   ）
    A、m＞3 B、m＝3 C、m＜3 D、m≤3

    查看试题解析

  • 7. 圆的直径是13cm，如果圆心与直线上某一点的距离是6.5cm，那么该直线和圆的位置关系是（   ）
    A、相离 B、相切 C、相交 D、相交或相切

    查看试题解析

  • 8. 如图，等边△ABC的边长为4，D，E，F分别为边AB，BC，AC的中点，分别以A，B，C三点为圆心，以AD长为半径作三条圆弧，则图中三条圆弧的弧长之和是（   ）

    A、π B、2π C、4π D、6π

    查看试题解析

  • 9. 如图，△ABC的内切圆与三边分别相切于点D，E，F，则下列等式：

    ①∠EDF＝∠B；②2∠EDF＝∠A＋∠C；③2∠A＝∠FED＋∠EDF；

    ④∠AED＋∠BFE＋∠CDF＝180°，其中成立的个数是（   ）

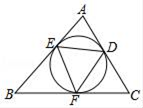    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 10. 二次函数y＝﹣x2﹣2x＋c在﹣3≤x≤2的范围内有最小值﹣5，则c的值是（   ）
    A、﹣6 B、﹣2 C、2 D、3

    查看试题解析

二、填空题

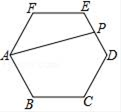
  • 11. 一元二次方程x2﹣a＝0的一个根是2，则a的值是 ．

    查看试题解析

  • 12. 把抛物线y＝2x2先向下平移1个单位，再向左平移2个单位，得到的抛物线的解析式是 ．

    查看试题解析

  • 13. 一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1、2、3、4．随机摸取一个小球然后放回，再随机摸出一个小球，两次取出的小球标号的和等于5的概率是 ．

    查看试题解析

  • 14. 设计人体雕像时，使雕像的上部（腰以上）与下部（腰以下）的高度比，等于下部与全部（全身）的高度比，可以增加视觉美感．按此比例，如果雕像的高为2m，那么上部应设计为多高？设雕像的上部高x m，列方程，并化成一般形式是 ．

    查看试题解析

  • 15. 如图，正六边形ABCDEF中，P是边ED的中点，连接AP，则 APAB ＝ ．

    查看试题解析

  • 16. 在⊙O中，弧AB所对的圆心角∠AOB＝108°，点C为⊙O上的动点，以AO、AC为边构造▱AODC．当∠A＝°时，线段BD最长．

    查看试题解析

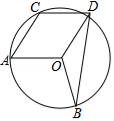
三、解答题

  • 17. 解方程：x2+x﹣3=0．

    查看试题解析

  • 18. 如图，在⊙O中，半径OA与弦BD垂直，点C在⊙O上，∠AOB=80°

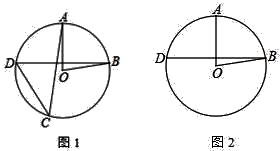    (1)、若点C在优弧BD上，求∠ACD的大小；
    (2)、若点C在劣弧BD上，直接写出∠ACD的大小．

    查看试题解析

  • 19. 甲、乙、丙三个盒子中分别装有除颜色外都相同的小球，甲盒中装有两个球，分别为一个红球和一个绿球；乙盒中装有三个球，分别为两个绿球和一个红球；丙盒中装有两个球，分别为一个红球和一个绿球，从三个盒子中各随机取出一个小球
    (1)、请画树状图，列举所有可能出现的结果
    (2)、请直接写出事件“取出至少一个红球”的概率．

    查看试题解析

  • 20. 如图，在平面直角坐标系中有点A（﹣4，0）、B（0，3）、P（a，﹣a）三点，线段CD与AB关于点P中心对称，其中A、B的对应点分别为C、D

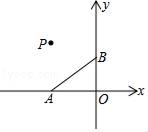    (1)、当a＝﹣4时

    ①在图中画出线段CD，保留作图痕迹。

    ②线段CD向下平移个单位时，四边形ABCD为菱形；

    (2)、当a＝时，四边形ABCD为正方形．

    查看试题解析

  • 21. 如图，点D在⊙O的直径AB的延长线上，CD切⊙O于点C，AE⊥CD于点E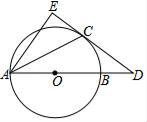

    (1)、求证：AC平分∠DAE；
    (2)、若AB＝6，BD＝2，求CE的长．

    查看试题解析

  • 22. 投资1万元围一个矩形菜园(如图)，其中一边靠墙，另外三边选用不同材料建造.墙长24 m，平行于墙的边的费用为200元/m，垂直于墙的边的费用为150元/m，设平行于墙的边长为x m.

    (1)、设垂直于墙的一边长为y m，直接写出y与x之间的函数关系式；
    (2)、若菜园面积为384 m2 ， 求x的值；
    (3)、求菜园的最大面积.

    查看试题解析

  • 23. 如图，点C为线段AB上一点，分别以AB、AC、CB为底作顶角为120°的等腰三角形，顶角顶点分别为D、E、F（点E、F在AB的同侧，点D在另一侧）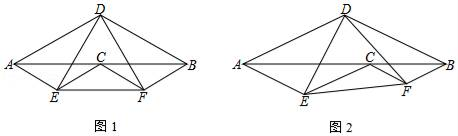

    (1)、如图1，若点C是AB的中点，则∠AED＝；
    (2)、如图2，若点C不是AB的中点

    ①求证：△DEF为等边三角形；

    ②连接CD，若∠ADC＝90°，AB＝3，请直接写出EF的长．

    查看试题解析

  • 24. 已知抛物线y＝ax2＋2x＋c与x轴交于A（﹣1，0）、B（3，0）两点，一次函数y＝kx＋b的图象l经过抛物线上的点C（m，n）
    (1)、求抛物线的解析式；
    (2)、若m＝3，直线l与抛物线只有一个公共点，求k的值；
    (3)、若k＝﹣2m＋2，直线l与抛物线的对称轴相交于点D，点P在对称轴上．当PD＝PC时，求点P的坐标．

    查看试题解析