河南省周口市沈丘县2018届九年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、单选题
-
1. 如果 ,则 =( )A、 B、
 C、
D、
2. 如图,直线OA与x轴的夹角为α,与双曲线y= (x>0)交于点A(1,α),则tanα的值为( )
C、
D、
2. 如图,直线OA与x轴的夹角为α,与双曲线y= (x>0)交于点A(1,α),则tanα的值为( ) A、4 B、3 C、2 D、63. 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为 ,AC=2,则sinB的值是( ).
A、4 B、3 C、2 D、63. 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为 ,AC=2,则sinB的值是( ).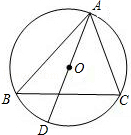 A、 B、 C、 D、4. 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则 的值为( )
A、 B、 C、 D、4. 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则 的值为( ) A、 B、 C、 D、5. 如图,A,B,C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )
A、 B、 C、 D、5. 如图,A,B,C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )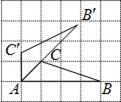 A、 B、 C、 D、
A、 B、 C、 D、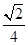 6. 如图,一次函数y1=x与二次函数y2=ax2+bx+c的图象相交于P,Q两点,则函数y=ax2+(b-1)x+c的图象可能是( )
6. 如图,一次函数y1=x与二次函数y2=ax2+bx+c的图象相交于P,Q两点,则函数y=ax2+(b-1)x+c的图象可能是( ) A、
A、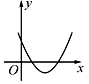 B、
B、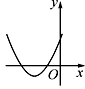 C、
C、 D、
D、 7. 二次函数y=ax2+bx+c(a≠0),自变量x与函数y的对应值如下表:则下列说法正确的是( )
7. 二次函数y=ax2+bx+c(a≠0),自变量x与函数y的对应值如下表:则下列说法正确的是( )x
…
﹣5
﹣4
﹣3
﹣2
﹣1
0
…
y
…
4.9
0.06
﹣2
﹣2
0.06
4.9
…
A、抛物线的开口向下 B、当x>﹣3时,y随x的增大而增大 C、二次函数的最大值是6 D、抛物线的对称轴是8. 如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为( ) A、4 B、5 C、6 D、79. 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A、4 B、5 C、6 D、79. 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )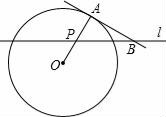 A、
A、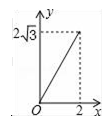 B、
B、 C、
C、 D、
D、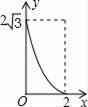 10. 如图,在△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图中阴影部分的面积为( )
10. 如图,在△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图中阴影部分的面积为( ) A、1 B、2 C、1+
A、1 B、2 C、1+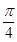 D、2﹣
D、2﹣ 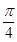
二、填空题
-
11. 如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为 .
 12. 已知二次函数y=-x2+4,当-2≤x≤3时,函数的最小值是 , 最大值是 .13. 如图,在边长为10cm的正方形ABCD中,P为AB边上任意一点(P不与A、B两点重合),连结DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为cm.
12. 已知二次函数y=-x2+4,当-2≤x≤3时,函数的最小值是 , 最大值是 .13. 如图,在边长为10cm的正方形ABCD中,P为AB边上任意一点(P不与A、B两点重合),连结DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为cm. 14. 已知抛物线 具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到 轴的距离始终相等,如图,点M的坐标为 ,P是抛物线 上一个动点,则△PMF周长的最小值是.
14. 已知抛物线 具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到 轴的距离始终相等,如图,点M的坐标为 ,P是抛物线 上一个动点,则△PMF周长的最小值是. 15. 如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2 , 交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C6 , 若点P(11,m)在第6段抛物线C6上,则m= .
15. 如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2 , 交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C6 , 若点P(11,m)在第6段抛物线C6上,则m= .
三、解答题
-
16. 有一座抛物线形拱桥,正常水位时桥下水面宽为20m,拱顶距水面4m.
 (1)、在如图的直角坐标系中,求出该抛物线的解析式;(2)、为保证过往船只顺利航行,桥下水面宽度不得小于18m,求水面在正常水位基础上,最多涨多少米,不会影响过往船只?17. 某经销商销售一种进价为每件10元的小商品.销售过程中发现:每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+400.(1)、设经销商每月获得的利润为W(元),求W与x之间的函数关系式(不要求写自变量x的取值范围)(2)、根据物价部门规定,这种小商品的销售单价不得高于23元,求经销商销售这种小商品每月获得的最大利润.(利润=售价﹣进价)18. 如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D、F分别在边AB、AC上.
(1)、在如图的直角坐标系中,求出该抛物线的解析式;(2)、为保证过往船只顺利航行,桥下水面宽度不得小于18m,求水面在正常水位基础上,最多涨多少米,不会影响过往船只?17. 某经销商销售一种进价为每件10元的小商品.销售过程中发现:每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+400.(1)、设经销商每月获得的利润为W(元),求W与x之间的函数关系式(不要求写自变量x的取值范围)(2)、根据物价部门规定,这种小商品的销售单价不得高于23元,求经销商销售这种小商品每月获得的最大利润.(利润=售价﹣进价)18. 如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D、F分别在边AB、AC上. (1)、求证:△BDE∽△CEF;(2)、当点E移动到BC的中点时,求证:FE平分∠DFC.19. 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)、求证:△BDE∽△CEF;(2)、当点E移动到BC的中点时,求证:FE平分∠DFC.19. 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.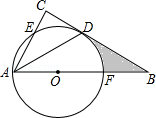 (1)、试判断直线BC与⊙O的位置关系,并说明理由;(2)、若BD=2 ,BF=2,求阴影部分的面积(结果保留π).20. 高中招生指标到校是我市中考招生制度改革的一项重要措施.某初级中学对该校近四年指标到校保送生人数进行了统计,制成了如下两幅不完整的统计图:
(1)、试判断直线BC与⊙O的位置关系,并说明理由;(2)、若BD=2 ,BF=2,求阴影部分的面积(结果保留π).20. 高中招生指标到校是我市中考招生制度改革的一项重要措施.某初级中学对该校近四年指标到校保送生人数进行了统计,制成了如下两幅不完整的统计图: (1)、该校近四年保送生人数的极差是W.请将折线统计图补充完整;(2)、该校2009年指标到校保送生中只有1位女同学,学校打算从中随机选出2位同学了解他们进入高中阶段的学习情况.请用列表法或画树状图的方法,求出所选两位同学恰好是1位男同学和1位女同学的概率.21. 如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A在同一水平线上,A、B、P、C在同一平面内.
(1)、该校近四年保送生人数的极差是W.请将折线统计图补充完整;(2)、该校2009年指标到校保送生中只有1位女同学,学校打算从中随机选出2位同学了解他们进入高中阶段的学习情况.请用列表法或画树状图的方法,求出所选两位同学恰好是1位男同学和1位女同学的概率.21. 如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A在同一水平线上,A、B、P、C在同一平面内. (1)、求居民楼AB的高度;(2)、求C、A之间的距离.
(1)、求居民楼AB的高度;(2)、求C、A之间的距离.(精确到0.1m,参考数据: ≈1.41, ≈1.73, ≈2.45)
22. 如图,抛物线y=﹣ +bx+c经过A(4,0),C(0,4)两点,点B是抛物线与x轴的另一个交点,点E是OC的中点,作直线AC、点M在抛物线上,过点M作MD⊥x轴,垂足为点D,交直线AC于点N,设点M的横坐标为m,MN的长度为d. (1)、直接写出直线AC的函数关系式;(2)、求抛物线对应的函数关系式;(3)、求d关于m的函数关系式;(4)、当以点M、N、E、O为顶点的四边形为平行四边形时,直接写出m的值.
(1)、直接写出直线AC的函数关系式;(2)、求抛物线对应的函数关系式;(3)、求d关于m的函数关系式;(4)、当以点M、N、E、O为顶点的四边形为平行四边形时,直接写出m的值.