河南省洛阳市嵩县2018届九年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、单选题
-
1. 二次根式 中,x的取值范围是( )A、x≥1 B、x>1 C、x≤1 D、x<12. 下列二次根式中,是最简二次根式的是( )A、
 B、
B、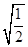 C、
C、 D、
D、 3. 下列运算正确的是( )A、
3. 下列运算正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为( )A、﹣1 B、1 C、1或﹣1 D、0.55. sin245°﹣3tan230°+4cos260°的值是( )A、0 B、 C、2 D、36. 如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,则AE的长为( )
4. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为( )A、﹣1 B、1 C、1或﹣1 D、0.55. sin245°﹣3tan230°+4cos260°的值是( )A、0 B、 C、2 D、36. 如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,则AE的长为( ) A、
A、 B、
C、3
D、
B、
C、3
D、 或
7. 如图,在直角梯形ABCD中,AD∥BC,∠B=90度,AC将梯形分成两个三角形,其中△ACD是周长为18cm的等边三角形,则该梯形的中位线的长是( )
或
7. 如图,在直角梯形ABCD中,AD∥BC,∠B=90度,AC将梯形分成两个三角形,其中△ACD是周长为18cm的等边三角形,则该梯形的中位线的长是( ) A、9cm B、12cm C、
A、9cm B、12cm C、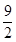 cm
D、18cm
8. 如图,已知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( )
cm
D、18cm
8. 如图,已知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( )①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.
 A、1 B、2 C、3 D、49. 从 ,0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是( )A、
A、1 B、2 C、3 D、49. 从 ,0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是( )A、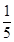 B、
B、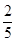 C、
C、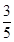 D、
10. 如图所示,已知:点A(0,0),B( ,0),C(0,1).在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于( )
D、
10. 如图所示,已知:点A(0,0),B( ,0),C(0,1).在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于( ) A、
A、 B、
B、 C、
C、 D、
D、 11. 在△ABC中,(tanA﹣ )2+| ﹣cosB|=0,则∠C的度数为 .12. 若 = ,则 = .13. 设a,b是方程x2+x﹣2011=0的两个实数根,则a2+2a+b的值为 .14. 如图,▱ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.若△DEF的面积为1,则▱ABCD的面积为
11. 在△ABC中,(tanA﹣ )2+| ﹣cosB|=0,则∠C的度数为 .12. 若 = ,则 = .13. 设a,b是方程x2+x﹣2011=0的两个实数根,则a2+2a+b的值为 .14. 如图,▱ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.若△DEF的面积为1,则▱ABCD的面积为 15. 如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB干点E,且tan∠α= ,有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或 ;④0<BE≤ .其中正确的结论是(填入正确结论的序号).
15. 如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB干点E,且tan∠α= ,有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或 ;④0<BE≤ .其中正确的结论是(填入正确结论的序号).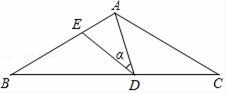
二、解答题
-
16. 计算(1)、|﹣3 |﹣2cos30°﹣ ﹣2﹣2+(3﹣π)0(2)、先化简,再求值,已知x=(2+ )2006( ﹣2)2007﹣ ,
求(1﹣ )÷ 的值.
17. 已知关于x的方程x2+ax+a﹣2=0.(1)、当该方程的一个根为1时,求a的值及该方程的另一根;(2)、求证:不论a取何实数,该方程都有两个不相等的实数根.18. 已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.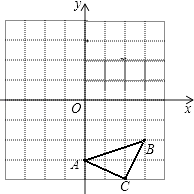
①画出△ABC向上平移6个单位得到的△A1B1C1;
②以点C为位似中心,在网格中画出△A2B2C2 , 使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.
19. 为进一步促进义务教育均衡发展,某市加大了基础教育经费的投入,已知2015年该市投入基础教育经费5000万元,2017年投入基础教育经费7200万元.(1)、求该市这两年投入基础教育经费的年平均增长率;(2)、如果按(1)中基础教育经费投入的年平均增长率计算,该市计划2018年用不超过当年基础教育经费的5%购买电脑和实物投影仪共1500台,调配给农村学校.若购买一台电脑需3500元,购买一台实物投影需2000元,则最多可购买电脑多少台?20. 如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米. (1)、求新传送带AC的长度;(2)、如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:(1)(2)的计算结果精确到0.1米,参考数据: ≈1.41, ≈1.73, ≈2.24, ≈2.45)21. 为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
(1)、求新传送带AC的长度;(2)、如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:(1)(2)的计算结果精确到0.1米,参考数据: ≈1.41, ≈1.73, ≈2.24, ≈2.45)21. 为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.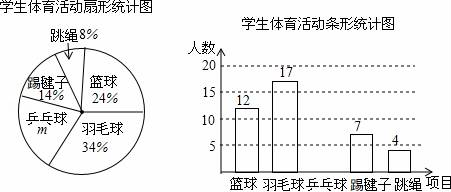 (1)、m=%,这次共抽取了名学生进行调查;并补全条形图;(2)、请你估计该校约有名学生喜爱打篮球;(3)、现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?22. 如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)、m=%,这次共抽取了名学生进行调查;并补全条形图;(2)、请你估计该校约有名学生喜爱打篮球;(3)、现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?22. 如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC. (1)、求证:△ADE∽△ABC;(2)、若AD=3,AB=5,求 的值.23. 如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒.
(1)、求证:△ADE∽△ABC;(2)、若AD=3,AB=5,求 的值.23. 如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒. (1)、当t=2时,求点E的坐标;(2)、若AB平分∠EBP时,求t的值.(3)、在运动的过程中,是否存在以P、O、E为顶点的三角形与△ABE相似.若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、当t=2时,求点E的坐标;(2)、若AB平分∠EBP时,求t的值.(3)、在运动的过程中,是否存在以P、O、E为顶点的三角形与△ABE相似.若存在,请求出点P的坐标;若不存在,请说明理由.