河南省洛阳市孟津县2018届九年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、单选题
-
1. 化简 的结果是( )A、 B、
 C、
C、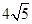 D、20
2. 一元二次方程2x2﹣5x﹣2=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. 用配方法解方程 时,经过配方,得到( )A、
D、20
2. 一元二次方程2x2﹣5x﹣2=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. 用配方法解方程 时,经过配方,得到( )A、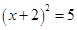 B、
B、 C、
C、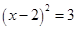 D、
D、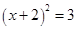 4. 某商场今年3月份的营业额为400万元,5月份的营业额达到633.6万元,若设商场3月份到5月份营业额的月平均增长率为x,则下面列出的方程中正确的是( )A、400(1+x)2=633.6 B、400(1+2x)2=6336 C、400×(1+2x)2=63.6 D、400×(1+x)2=633.6+4005. 当A为锐角,且<cosA<时,∠A的范围是( )A、0°<∠A<30° B、30°<∠A<60° C、60°<∠A<90° D、30°<∠A<45°6. 如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
4. 某商场今年3月份的营业额为400万元,5月份的营业额达到633.6万元,若设商场3月份到5月份营业额的月平均增长率为x,则下面列出的方程中正确的是( )A、400(1+x)2=633.6 B、400(1+2x)2=6336 C、400×(1+2x)2=63.6 D、400×(1+x)2=633.6+4005. 当A为锐角,且<cosA<时,∠A的范围是( )A、0°<∠A<30° B、30°<∠A<60° C、60°<∠A<90° D、30°<∠A<45°6. 如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )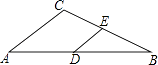 A、8 B、10 C、12 D、147. 如图1,在三角形纸片ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形相似的有( )
A、8 B、10 C、12 D、147. 如图1,在三角形纸片ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形相似的有( )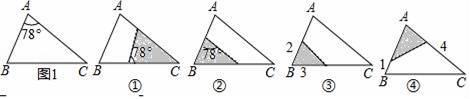 A、①②③ B、①②④ C、①③④ D、②③④8.
A、①②③ B、①②④ C、①③④ D、②③④8.一个不透明的袋子里有若干个小球,它们除了颜色外,其它都相同,甲同学从袋子里随机摸出一个球,记下颜色后放回袋子里,摇匀后再次随机摸出一个球,记下颜色,…,甲同学反复大量实验后,根据白球出现的频率绘制了如图所示的统计图,则下列说法正确的是( )
 A、袋子一定有三个白球 B、袋子中白球占小球总数的十分之三 C、再摸三次球,一定有一次是白球 D、再摸1000次,摸出白球的次数会接近330次9. 如图,面积为16的正方形ABCD中,有一个小正方形EFGH,其中E,F,G分别在AB,BC,FD上.若BF=1,则小正方形的周长为( )
A、袋子一定有三个白球 B、袋子中白球占小球总数的十分之三 C、再摸三次球,一定有一次是白球 D、再摸1000次,摸出白球的次数会接近330次9. 如图,面积为16的正方形ABCD中,有一个小正方形EFGH,其中E,F,G分别在AB,BC,FD上.若BF=1,则小正方形的周长为( )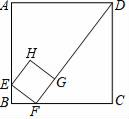 A、7 B、6 C、5 D、410. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
A、7 B、6 C、5 D、410. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )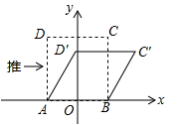 A、( ,1) B、(2,1) C、(1, ) D、(2, )
A、( ,1) B、(2,1) C、(1, ) D、(2, )二、填空题
-
11. 二次根式 有意义,则x取值范围 .12. 已知a:b=3:2,则(a-b):a= .
13. 有画有等腰三角形、平行四边形、等腰梯形、长方形、等边三角形五张卡片,背面朝下,颜色、形状、大小都一样,任取一张是中心对称图形的概率是 .14. 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为 . 15. 如图,D是等边△ABC边AB上的点,AD=2,DB=4.现将△ABC折叠,使得点C与点D重合,折痕为EF,且点E、F分别在边AC和BC上,则 = .
15. 如图,D是等边△ABC边AB上的点,AD=2,DB=4.现将△ABC折叠,使得点C与点D重合,折痕为EF,且点E、F分别在边AC和BC上,则 = .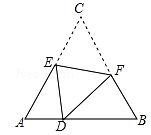 16. 如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为米(结果保留根号).
16. 如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为米(结果保留根号).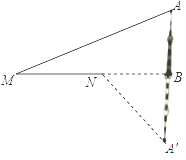
三、解答题
-
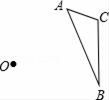
17. 计算: .18. 如图,以O为位似中心,将△ABC放大为原来的2倍(不写作法,保留作图痕迹).
 19. 已知关于x方程2x2﹣(3+4k)x+2k2+k=0,k为何值时,方程有两个不相等的实数根?20. 如图,某旅游景点要在长、宽分别为20米、12米的矩形水池的正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四角连接四条与矩形的边互相平行且宽度相等的道路,已知道路的宽为正方形边长的 ,若道路与观赏亭的面积之和是矩形水池面积的 ,求道路的宽.
19. 已知关于x方程2x2﹣(3+4k)x+2k2+k=0,k为何值时,方程有两个不相等的实数根?20. 如图,某旅游景点要在长、宽分别为20米、12米的矩形水池的正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四角连接四条与矩形的边互相平行且宽度相等的道路,已知道路的宽为正方形边长的 ,若道路与观赏亭的面积之和是矩形水池面积的 ,求道路的宽. 21. 甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传三次.(1)、求三次传球后,球回到甲脚下的概率;(2)、三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?22. 如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.
21. 甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传三次.(1)、求三次传球后,球回到甲脚下的概率;(2)、三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?22. 如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D. (1)、求证:FB2=FE•FA;(2)、若BF=3,EF=2,求△ABE与△BEF的面积之比.、23. 已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题:
(1)、求证:FB2=FE•FA;(2)、若BF=3,EF=2,求△ABE与△BEF的面积之比.、23. 已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题: (1)、当t为何值时,PQ∥AB?(2)、当t=3时,求△QMC的面积;(3)、是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由
(1)、当t为何值时,PQ∥AB?(2)、当t=3时,求△QMC的面积;(3)、是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由