河南省洛阳市洛宁县2018届九年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、单选题
-
1. 化简 的结果是( )A、 B、
 C、
C、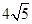 D、
D、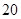 2. 一元二次方程2x2﹣5x﹣2=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. 用配方法解方程 x2+4x+1=0 时,经过配方,得到( )
2. 一元二次方程2x2﹣5x﹣2=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. 用配方法解方程 x2+4x+1=0 时,经过配方,得到( )
A、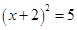 B、
B、 C、
C、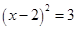 D、
D、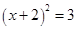 4. 某商场今年3月份的营业额为400万元,5月份的营业额达到633.6万元,若设商场3月份到5月份营业额的月平均增长率为x,则下面列出的方程中正确的是( )A、400(1+x)2=633.6 B、400(1+2x)2=6336 C、400×(1+2x)2=63.6 D、400×(1+x)2=633.6+4005. 当A为锐角,且<cosA<时,∠A的范围是( )A、0°<∠A<30° B、30°<∠A<60° C、60°<∠A<90° D、30°<∠A<45°6. 如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
4. 某商场今年3月份的营业额为400万元,5月份的营业额达到633.6万元,若设商场3月份到5月份营业额的月平均增长率为x,则下面列出的方程中正确的是( )A、400(1+x)2=633.6 B、400(1+2x)2=6336 C、400×(1+2x)2=63.6 D、400×(1+x)2=633.6+4005. 当A为锐角,且<cosA<时,∠A的范围是( )A、0°<∠A<30° B、30°<∠A<60° C、60°<∠A<90° D、30°<∠A<45°6. 如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )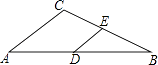 A、8 B、10 C、12 D、147. 如图1,在三角形纸片ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形相似的有( )
A、8 B、10 C、12 D、147. 如图1,在三角形纸片ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形相似的有( )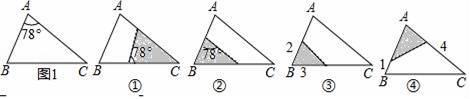 A、①②③ B、①②④ C、①③④ D、②③④8.
A、①②③ B、①②④ C、①③④ D、②③④8.一个不透明的袋子里有若干个小球,它们除了颜色外,其它都相同,甲同学从袋子里随机摸出一个球,记下颜色后放回袋子里,摇匀后再次随机摸出一个球,记下颜色,…,甲同学反复大量实验后,根据白球出现的频率绘制了如图所示的统计图,则下列说法正确的是( )
 A、袋子一定有三个白球 B、袋子中白球占小球总数的十分之三 C、再摸三次球,一定有一次是白球 D、再摸1000次,摸出白球的次数会接近330次9. 如图,面积为16的正方形ABCD中,有一个小正方形EFGH,其中E,F,G分别在AB,BC,FD上.若BF=1,则小正方形的周长为( )
A、袋子一定有三个白球 B、袋子中白球占小球总数的十分之三 C、再摸三次球,一定有一次是白球 D、再摸1000次,摸出白球的次数会接近330次9. 如图,面积为16的正方形ABCD中,有一个小正方形EFGH,其中E,F,G分别在AB,BC,FD上.若BF=1,则小正方形的周长为( )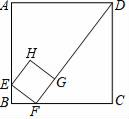 A、7 B、6 C、5 D、410. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
A、7 B、6 C、5 D、410. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )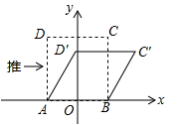 A、 ( ,1) B、(2,1) C、 (1, ) D、 (2, )11. 在Rt△ABC中,D为斜边AB的中点,且BC=3,AC=4,则线段CD的长是( )A、2 B、3 C、 D、512. 计算 的值等于( )A、
A、 ( ,1) B、(2,1) C、 (1, ) D、 (2, )11. 在Rt△ABC中,D为斜边AB的中点,且BC=3,AC=4,则线段CD的长是( )A、2 B、3 C、 D、512. 计算 的值等于( )A、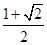 B、
B、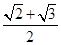 C、
C、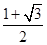 D、
13. 在Rt△ABC中,∠C=90°,AB=4, AC=1,则cosB的值为( )A、
D、
13. 在Rt△ABC中,∠C=90°,AB=4, AC=1,则cosB的值为( )A、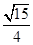 B、
C、
B、
C、 D、
D、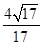 14. 一个不透明的盒子中装有6个大小相同的乒乓球,其中4个是黄球,2个是白球.从该盒子中任意摸出一个球,摸到黄球的概率是( )A、 B、 C、 D、
14. 一个不透明的盒子中装有6个大小相同的乒乓球,其中4个是黄球,2个是白球.从该盒子中任意摸出一个球,摸到黄球的概率是( )A、 B、 C、 D、 15. 同时投掷两枚硬币,出现两枚都是正面朝上的概率是( )A、 B、 C、1 D、16. 一副完整的扑克牌,去掉大小王,将剩余的52张混合后从中随机抽取一张,则抽出A的概率是( )A、 B、
15. 同时投掷两枚硬币,出现两枚都是正面朝上的概率是( )A、 B、 C、1 D、16. 一副完整的扑克牌,去掉大小王,将剩余的52张混合后从中随机抽取一张,则抽出A的概率是( )A、 B、 C、
C、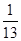 D、
D、 17. 要由抛物线 平移得到 ,则平移的方法是( )A、向左平移1个单位 B、向上平移1个单位 C、向下平移1个单位 D、向右平移1个单位18. 在二次函数 的图象中,若 随 的增大而增大,则 的取值范围是( )A、x<1 B、x>1 C、x<-1 D、x>-119. 抛物线y=(x﹣1)2+t与x轴的两个交点之间的距离为4,则t的值是( )A、﹣1 B、﹣2 C、﹣3 D、﹣4
17. 要由抛物线 平移得到 ,则平移的方法是( )A、向左平移1个单位 B、向上平移1个单位 C、向下平移1个单位 D、向右平移1个单位18. 在二次函数 的图象中,若 随 的增大而增大,则 的取值范围是( )A、x<1 B、x>1 C、x<-1 D、x>-119. 抛物线y=(x﹣1)2+t与x轴的两个交点之间的距离为4,则t的值是( )A、﹣1 B、﹣2 C、﹣3 D、﹣4二、填空题
-
20. 二次根式 有意义,则x取值范围 .21. 已知a:b=3:2,则(a-b):a= .
22. 有画有等腰三角形、平行四边形、等腰梯形、长方形、等边三角形五张卡片,背面朝下,颜色、形状、大小都一样,任取一张是中心对称图形的概率是 .23. 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为 . 24. 如图,D是等边△ABC边AB上的点,AD=2,DB=4.现将△ABC折叠,使得点C与点D重合,折痕为EF,且点E、F分别在边AC和BC上,则 = .
24. 如图,D是等边△ABC边AB上的点,AD=2,DB=4.现将△ABC折叠,使得点C与点D重合,折痕为EF,且点E、F分别在边AC和BC上,则 = .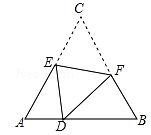 25. 如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为米(结果保留根号).
25. 如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为米(结果保留根号).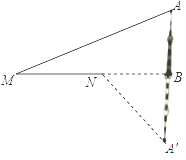 26. 点(2+a,3)关于y轴对称的点的坐标是(﹣4,2﹣b),则ab= .27. 已知:直角三角形ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,AC=CE=10cm,则BD= .
26. 点(2+a,3)关于y轴对称的点的坐标是(﹣4,2﹣b),则ab= .27. 已知:直角三角形ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,AC=CE=10cm,则BD= .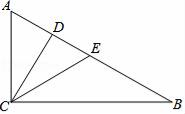 28. 直角三角形两锐角平分线相交所成的角的度数为。29. 写一个你喜欢的实数m的值 , 使得事件“对于二次函数y= x2﹣(m﹣1)x+3,当x<﹣3时,y随x的增大而减小”成为随机事件.30. 如图,管中放置着三根同样的绳子AA1、BB1、CC1 . 小明在左侧选两个打一个结,小红在右侧选两个打一个结,则这三根绳子能连结成一根长绳的概率为 .
28. 直角三角形两锐角平分线相交所成的角的度数为。29. 写一个你喜欢的实数m的值 , 使得事件“对于二次函数y= x2﹣(m﹣1)x+3,当x<﹣3时,y随x的增大而减小”成为随机事件.30. 如图,管中放置着三根同样的绳子AA1、BB1、CC1 . 小明在左侧选两个打一个结,小红在右侧选两个打一个结,则这三根绳子能连结成一根长绳的概率为 .
三、解答
-
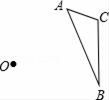
31. 计算: .32. 如图,以O为位似中心,将△ABC放大为原来的2倍(不写作法,保留作图痕迹).
 33. 已知关于x方程2x2﹣(3+4k)x+2k2+k=0,k为何值时,方程有两个不相等的实数根?34. 如图,某旅游景点要在长、宽分别为20米、12米的矩形水池的正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四角连接四条与矩形的边互相平行且宽度相等的道路,已知道路的宽为正方形边长的 ,若道路与观赏亭的面积之和是矩形水池面积的 ,求道路的宽.
33. 已知关于x方程2x2﹣(3+4k)x+2k2+k=0,k为何值时,方程有两个不相等的实数根?34. 如图,某旅游景点要在长、宽分别为20米、12米的矩形水池的正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四角连接四条与矩形的边互相平行且宽度相等的道路,已知道路的宽为正方形边长的 ,若道路与观赏亭的面积之和是矩形水池面积的 ,求道路的宽. 35. 甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传三次.(1)、求三次传球后,球回到甲脚下的概率;(2)、三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?36. 如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.
35. 甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传三次.(1)、求三次传球后,球回到甲脚下的概率;(2)、三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?36. 如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D. (1)、求证:FB2=FE•FA;(2)、若BF=3,EF=2,求△ABE与△BEF的面积之比.37. 已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题:
(1)、求证:FB2=FE•FA;(2)、若BF=3,EF=2,求△ABE与△BEF的面积之比.37. 已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题: (1)、当t为何值时,PQ∥AB?(2)、当t=3时,求△QMC的面积;(3)、是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由38.(1)、计算:2sin30°+4cos30°•tan60°﹣cos245°;(2)、抛物线y=ax2+bx+c经过点(0,0),(6,0),且抛物线最高点的纵坐标为3,求这条抛物线的解析式.39.
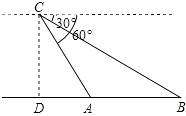
(1)、当t为何值时,PQ∥AB?(2)、当t=3时,求△QMC的面积;(3)、是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由38.(1)、计算:2sin30°+4cos30°•tan60°﹣cos245°;(2)、抛物线y=ax2+bx+c经过点(0,0),(6,0),且抛物线最高点的纵坐标为3,求这条抛物线的解析式.39.某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
 40. 第20届世界杯足球赛正在如火如荼的进行,爸爸想通过一个游戏决定小明能否看今晚的比赛:在一个不透明的盒子中放入三张卡片,每张卡片上写着一个实数,分别为3, , 2 (每张卡片除了上面的实数不同以外其余均相同),爸爸让小明从中任意取一张卡片,如果抽到的卡片上的数是有理数,就让小明看比赛,否则就不能看.(1)、请你直接写出按照爸爸的规则小明能看比赛的概率;(2)、小明想了想,和爸爸重新约定游戏规则:自己从盒子中随机抽取两次,每次抽取一张卡片,第一次抽取后记下卡片上的数,再将卡片放回盒中抽取第二次,如果抽取的两数之积是有理数,自己就看比赛,否则就不看.请你用列表法或树状图法求出按照此规则小明看比赛的概率.41. 为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
40. 第20届世界杯足球赛正在如火如荼的进行,爸爸想通过一个游戏决定小明能否看今晚的比赛:在一个不透明的盒子中放入三张卡片,每张卡片上写着一个实数,分别为3, , 2 (每张卡片除了上面的实数不同以外其余均相同),爸爸让小明从中任意取一张卡片,如果抽到的卡片上的数是有理数,就让小明看比赛,否则就不能看.(1)、请你直接写出按照爸爸的规则小明能看比赛的概率;(2)、小明想了想,和爸爸重新约定游戏规则:自己从盒子中随机抽取两次,每次抽取一张卡片,第一次抽取后记下卡片上的数,再将卡片放回盒中抽取第二次,如果抽取的两数之积是有理数,自己就看比赛,否则就不看.请你用列表法或树状图法求出按照此规则小明看比赛的概率.41. 为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别
分组 单位:元
人数
A
4
B
16
C
a
D
b
E
2
请根据以上图表,解答下列问题:
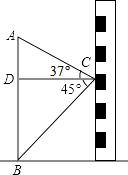
(1)、填空:这次被调查的同学共有人, , ;(2)、求扇形统计图中扇形C的圆心角度数;(3)、该校共有学生1000人,请估计每月零花钱的数额x在 范围的人数.42. 在一个口袋里装着白、红、黑三种颜色的小球(除颜色外形状大小完全相同),其中白球3个、红球2个、黑球1个.(1)、随机从袋中取出一个球,求取出的球是黑球的概率;(2)、若取出的第一只球是红球,不将它放回袋里,从袋中余下的球中再随机地取出1个,这时取出的球是黑球的概率是多少?(3)、若取出一个球,将它放回袋中,从袋中再随机地取出一个球,两次取出的球都是白球的概率是多少?(用列表法或树状图计算)43.如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
 44. “天天乐”商场销售一种进价为20元/台的台灯,经调查发现,该台灯每天的销售量w(台)与销售单价x(元)满足 ,设销售这种台灯每天的利润为y(元).(1)、求y与x之间的函数关系式;(2)、当销售单价定为多少元时,每天的利润最大?最大利润是多少?(3)、在保证销售量尽可能大的前提下,该商场每天还想获得150元的利润,应该将销售单价定为多少元?45. 如图,二次函数 (a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
44. “天天乐”商场销售一种进价为20元/台的台灯,经调查发现,该台灯每天的销售量w(台)与销售单价x(元)满足 ,设销售这种台灯每天的利润为y(元).(1)、求y与x之间的函数关系式;(2)、当销售单价定为多少元时,每天的利润最大?最大利润是多少?(3)、在保证销售量尽可能大的前提下,该商场每天还想获得150元的利润,应该将销售单价定为多少元?45. 如图,二次函数 (a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4). (1)、求二次函数的解析式和直线BD的解析式;(2)、点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;(3)、在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为 ?若存在求出点Q的坐标;若不存在请说明理由.
(1)、求二次函数的解析式和直线BD的解析式;(2)、点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;(3)、在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为 ?若存在求出点Q的坐标;若不存在请说明理由.