2018-2019学年初中数学北师大版八年级下册第一章 三角形的证明 单元测试B
试卷更新日期：2019-01-24 类型：单元试卷
一、选择题
-
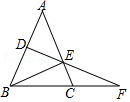
1. 等腰三角形一腰上的高与另一腰的夹角是50°，则这个等腰三角形的底角为（ ）A、70° B、20° C、70°或20° D、40°或140°2. 如图，在△ABC中，AB=AC，点D，E分别在边BC和AC上，若AD=AE，则下列结论错误的是（ ）
A、∠ADB=∠ACB+∠CAD B、∠ADE=∠AED C、∠B=∠C D、∠BAD=∠BDA3. 用一条长为16cm的细绳围成一个等腰三角形，若其中有一边的长为4cm，则该等腰三角形的腰长为（ ）A、4cm B、6cm C、4cm或6cm D、4cm或8cm4. 如图，四边形ABCD中，∠A=∠C=90°，∠B=60°，AD=1，BC=2，则四边形ABCD的面积是（ ）
A、
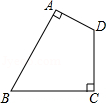B、3
C、
D、4
5. 如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为D，点E是AB的中点，CD=DE=a，则AB的长为（ ）
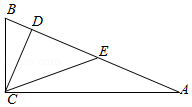A、2a B、2 a C、3a D、
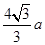6. 如图，在△ABC中，∠C=90°，∠B=30°，边AB的垂直平分线DE交AB于点E，交BC于点D，CD=3，则BC的长为（ ）
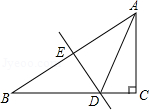A、6 B、6 C、9 D、37.将一副直角三角尺如图放置，若∠AOD=20°，则∠BOC的大小为（ ）
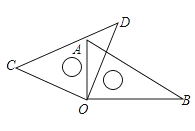A、140° B、160° C、170° D、150°8. 如图所示，线段AC的垂直平分线交线段AB于点D，∠A=50°，则∠BDC=（ ）
A、50° B、100° C、120° D、130°9. 如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A=60°，∠ABD=24°，则∠ACF的度数为（ ）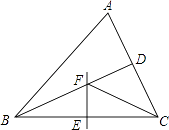
A、48° B、36° C、30° D、24°10. 如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD=8，则点P到BC的距离是（ ）
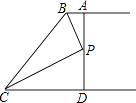A、8 B、6 C、4 D、211. 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（ ）
A、10 B、7 C、5 D、4二、填空题
-
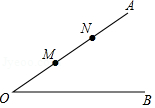
12. 如图，∠AOB=45°，点M，N在边OA上，OM=x，ON=x+4，点P是边OB上的点．若使点P，M，N构成等腰三角形的点P恰好有三个，则x的值是 ．
13. 如图，在四边形ABCD中，∠ABC=∠ADC=90°，E为对角线AC的中点，连接BE，ED，BD．若∠BAD=58°，则∠EBD的度数为度．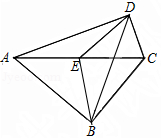
14. 如图，已知在△ABC中，DE是BC的垂直平分线，垂足为E，交AC于点D，若AB=6，AC=9，则△ABD的周长是 ．
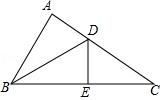15. 如图所示，在△ABC中，∠BAC=106°，EF、MN分别是AB、AC的垂直平分线，点E、N在BC上，则∠EAN= ．
16. 如图，AD⊥BC，BD=CD，点C在AE的垂直平分线上，已知BD=2，AB=4，则DE= ．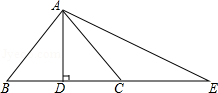
三、解答题
-
17. 如图，在△ABC中，∠BAC=90°，AB=AC，点D在BC上，且BD=BA，点E在BC的延长线上，且CE=CA．
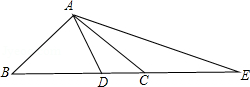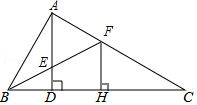
(1)、试求∠DAE的度数．(2)、如果把原题中“AB=AC”的条件去掉，其余条件不变，那么∠DAE的度数会改变吗？为什么？18. 如图，在△ABC中，AB=AC，点E在CA的延长线上，EP⊥BC，垂足为P，EP交AB于点F，FD∥AC交BC于点D．求证：△AEF是等腰三角形．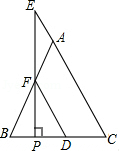
19. 如图1，已知∠ABC=90°，△ABC是等腰三角形，点D为斜边AC的中点，连接DB，过点A作∠BAC的平分线，分别与DB，BC相交于点E，F．
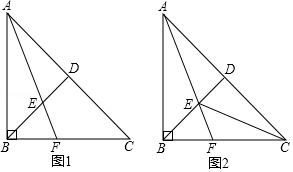(1)、求证：BE=BF；(2)、如图2，连接CE，在不添加任何辅助线的条件下，直接写出图中所有的等腰三角形．20. 在等腰△ABC中，AB=AC=8，∠BAC=100°，AD是∠BAC的平分线，交BC于D，点E是AB的中点，连接DE．
(1)、求∠BAD的度数；(2)、求∠B的度数；(3)、求线段DE的长．
