2018-2019学年初中数学北师大版八年级下册第一章 三角形的证明 单元测试A
试卷更新日期:2019-01-24 类型:单元试卷
一、选择题
-
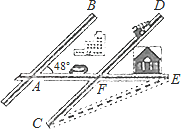
1. 到三角形三个顶点的距离都相等的点是这个三角形的( )A、三条高的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条边的垂直平分线的交点2. 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )
 A、48° B、40° C、30° D、24°3. 若等腰三角形的周长为10 cm,其中一边长为2 cm,则该等腰三角形的底边长为( )A、2 cm B、4 cm C、6 cm D、8 cm4. 已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )条.A、3 B、4 C、5 D、65.
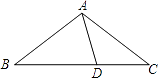
A、48° B、40° C、30° D、24°3. 若等腰三角形的周长为10 cm,其中一边长为2 cm,则该等腰三角形的底边长为( )A、2 cm B、4 cm C、6 cm D、8 cm4. 已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )条.A、3 B、4 C、5 D、65.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
 A、40° B、36° C、30° D、25°6. 如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=( )
A、40° B、36° C、30° D、25°6. 如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=( )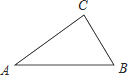 A、6 B、6 C、6 D、127. 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
A、6 B、6 C、6 D、127. 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )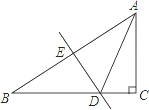 A、6 B、6 C、9 D、38. 如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=( )
A、6 B、6 C、9 D、38. 如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=( ) A、50° B、100° C、120° D、130°9. 如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
A、50° B、100° C、120° D、130°9. 如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( ) A、13 B、15 C、17 D、1910. 如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
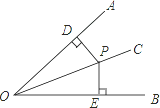
A、13 B、15 C、17 D、1910. 如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )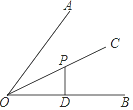 A、1 B、2 C、 D、411. 如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,则PD等于( )
A、1 B、2 C、 D、411. 如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,则PD等于( )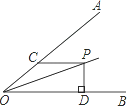 A、1 B、2 C、4 D、8
A、1 B、2 C、4 D、8二、填空题
-
12. 如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a、b的代数式表示△ABC的周长为 .
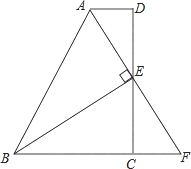
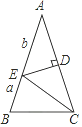 13. 如图,已知Rt△ABE中∠A=90°,∠B=60°,BE=10,D是线段AE上的一动点,过D作CD交BE于C,并使得∠CDE=30°,则CD长度的取值范围是 .
13. 如图,已知Rt△ABE中∠A=90°,∠B=60°,BE=10,D是线段AE上的一动点,过D作CD交BE于C,并使得∠CDE=30°,则CD长度的取值范围是 .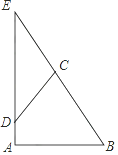 14. 如图,已知在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是 .
14. 如图,已知在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是 .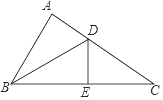 15. 如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=度.
15. 如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=度.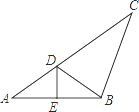 16. 如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是 .
16. 如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是 .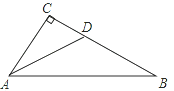 17. 如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .
17. 如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .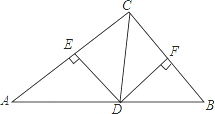
三、解答题
-
18. 如图,AD平分∠BAC,AD⊥BD,垂足为点D,DE∥AC.
求证:△BDE是等腰三角形.
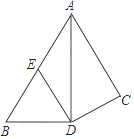 19. 如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
19. 如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.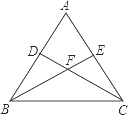 (1)、判断∠ABE与∠ACD的数量关系,并说明理由;(2)、求证:过点A、F的直线垂直平分线段BC.20. 如图,△ABC中,AB=AC,D点在BC上,∠BAD=30°,且∠ADC=60°.请完整说明为何AD=BD与CD=2BD的理由.
(1)、判断∠ABE与∠ACD的数量关系,并说明理由;(2)、求证:过点A、F的直线垂直平分线段BC.20. 如图,△ABC中,AB=AC,D点在BC上,∠BAD=30°,且∠ADC=60°.请完整说明为何AD=BD与CD=2BD的理由.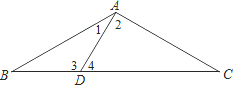 21. 如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.
21. 如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.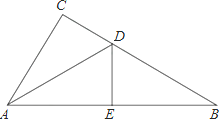 22. 如图,四边形ABCD中,AC为∠BAD的角平分线,AB=AD,E、F两点分别在AB、AD上,且AE=DF.请完整说明为何四边形AECF的面积为四边形ABCD的一半.
22. 如图,四边形ABCD中,AC为∠BAD的角平分线,AB=AD,E、F两点分别在AB、AD上,且AE=DF.请完整说明为何四边形AECF的面积为四边形ABCD的一半.