2018-2019学年初中数学北师大版八年级下册第二章 一元一次不等式与一元一次不等式组 单元测试A
试卷更新日期：2019-01-24 类型：单元试卷
一、选择题
-
1. 已知实数a，b满足a+1＞b+1，则下列不符合题意的为（ ）A、a＞b B、a+2＞b+2 C、﹣a＜﹣b D、2a＞3b2. 若实数3是不等式2x﹣a﹣2＜0的一个解，则a可取的最小正整数为（ ）A、2 B、3 C、4 D、53. 将不等式组 的解集表示在数轴上，下面表示正确的是（ ）A、
B、
C、
D、
4. 关于x的一元一次不等式 ≤﹣2的解集为x≥4，则m的值为（ ）A、14 B、7 C、﹣2 D、25. 若关于x的不等式组 的整数解共有3个，则m的取值范围是（ ）A、5＜m＜6 B、5＜m≤6 C、5≤m≤6 D、5≤m＜66.运行程序如图所示，规定：从“输入一个值x”到“结果是否＞95”为一次程序操作，如果程序操作进行了三次才停止，那么x的取值范围是（ ）
A、x≥11 B、11≤x＜23 C、11＜x≤23 D、x≤237. 宜宾市某化工厂，现有A种原料52千克，B种原料64千克，现用这些原料生产甲、乙两种产品共20件．已知生产1件甲种产品需要A种原料3千克，B种原料2千克；生产1件乙种产品需要A种原料2千克，B种原料4千克，则生产方案的种数为（ ）A、4 B、5 C、6 D、78. 如图，函数y1=﹣2x与y2=ax+3的图象相交于点A（m，2），则关于x的不等式﹣2x＞ax+3的解集是（ ）
A、x＞2 B、x＜2 C、x＞﹣1 D、x＜﹣1二、填空题
-
9. 商家花费760元购进某种水果80千克，销售中有5%的水果正常损耗．为了避免亏本，售价至少应定为元/千克．10. 如图，直线y=kx和y=ax+4交于A（1，k），则不等式kx﹣6＜ax+4＜kx的解集为 ．
11. 不等式组 的整数解是 ．12. 对非负实数x“四舍五入”到个位的值记为（x）．即当n为非负整数时，若n﹣ ≤x＜n+ ，则（x）=n．如（0.46）=0，（3.67）=4．给出下列关于（x）的结论：
①（1.493）=1；②（2x）=2（x）；③若（ ）=4，则实数x的取值范围是9≤x＜11；④当x≥0，m为非负整数时，有（m+2013x）=m+（2013x）；⑤（x+y）=（x）+（y）；其中，正确的结论有（填写所有正确的序号）．
三、解答题
-
13. 解不等式：(1)、 ≤ ．(2)、解不等式 ﹣1≤ ，并把解集在数轴上表示出来．
14. 解不等式组：(1)、 ．(2)、 ，并将它的解集在数轴上表示出来．15. 对于任意实数a，b，定义关于“⊗”的一种运算如下：a⊗b=2a﹣b．例如：5⊗2=2×5﹣2=8，（﹣3）⊗4=2×（﹣3）﹣4=﹣10．(1)、若3⊗x=﹣2011，求x的值；(2)、若x⊗3＜5，求x的取值范围．16. 已知关于x的不等式 ＞ x﹣1．
(1)、当m=1时，求该不等式的解集；(2)、m取何值时，该不等式有解，并求出解集．17. 如图，已知直线y1=﹣ x+1与x轴交于点A，与直线y2=﹣ x交于点B．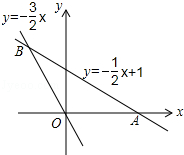
(1)、求△AOB的面积；(2)、求y1＞y2时x的取值范围．18. 某大型快递公司使用机器人进行包裹分拣，若甲机器人工作2h，乙机器人工作4h，一共可以分拣700件包裹；若甲机器人工作3h，乙机器人工作2h，一共可以分拣650件包裹．(1)、求甲、乙两机器人每小时各分拣多少件包裹；(2)、“双十一”期间，快递公司的业务量猛增，要让甲、乙两机器人每天分拣包裹的总数量不低于2250件，它们每天至少要一起工作多少小时？19. 为积极响应政府提出的“绿色发展•低碳出行”号召，某社区决定购置一批共享单车．经市场调查得知，购买3辆男式单车与4辆女式单车费用相同，购买5辆男式单车与4辆女式单车共需16000元．(1)、求男式单车和女式单车的单价；(2)、该社区要求男式单车比女式单车多4辆，两种单车至少需要22辆，购置两种单车的费用不超过50000元，该社区有几种购置方案？怎样购置才能使所需总费用最低，最低费用是多少？