浙江省台州市椒江区2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、选择题
-
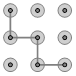
1. 下列手机手势解锁图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、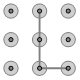 D、
D、 2. 下列关于反比例函数 的说法不正确的是( )A、其图象经过点(-2,1) B、其图象位于第二、第四象限 C、当x<0时,y随x增大而增大 D、当x>-1时,y>23. 下列说法中错误的是( )A、概率很小的事件不可能发生 B、不可能事件发生的概率为0 C、随机事件发生的概率大于或等于0且小于或等于1 D、必然事件发生的概率为14. 如图,在平面直角坐标系中,其中一个三角形是由另一个三角形绕某点旋转一定的角度得到的,则其旋转中心是( )
2. 下列关于反比例函数 的说法不正确的是( )A、其图象经过点(-2,1) B、其图象位于第二、第四象限 C、当x<0时,y随x增大而增大 D、当x>-1时,y>23. 下列说法中错误的是( )A、概率很小的事件不可能发生 B、不可能事件发生的概率为0 C、随机事件发生的概率大于或等于0且小于或等于1 D、必然事件发生的概率为14. 如图,在平面直角坐标系中,其中一个三角形是由另一个三角形绕某点旋转一定的角度得到的,则其旋转中心是( )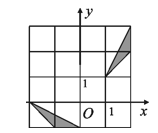 A、(1,0) B、(-1,2) C、(0,0) D、(-1,1)5. 某种植物的主干长出若干个数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是111,求每个支干长出多少个小分支?解:设主干长出x个支干,每个支干有x个小分支,由题意,所列方程正确的是( )A、
A、(1,0) B、(-1,2) C、(0,0) D、(-1,1)5. 某种植物的主干长出若干个数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是111,求每个支干长出多少个小分支?解:设主干长出x个支干,每个支干有x个小分支,由题意,所列方程正确的是( )A、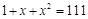 B、
B、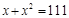 C、
C、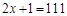 D、
D、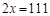 6. 如图,A,B两点在双曲线 上,分别经过A,B两点向坐标轴作垂线段,已知S阴影=1.7,则S1+S2等于( )
6. 如图,A,B两点在双曲线 上,分别经过A,B两点向坐标轴作垂线段,已知S阴影=1.7,则S1+S2等于( )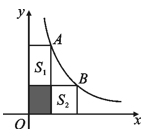 A、4 B、4.2 C、4.6 D、57. 小张承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有一种苹果树苗,它的
A、4 B、4.2 C、4.6 D、57. 小张承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有一种苹果树苗,它的成活率如下表所示:
移植棵数(n)
成活数(m)
成活率(m/n)
移植棵数(n)
成活数(m)
成活率(m/n)
50
47
0.940
1500
1335
0.890
270
235
0.870
3500
3203
0.915
400
369
0.923
7000
6335
0.905
750
662
0.883
14000
12628
0.902
下面有四个推断:
①当移植的树数是1 500时,表格记录成活数是1 335,所以这种树苗成活的概率是0.890;②随着移植棵数的增加,树苗成活的频率总在0.900附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是0.900;③若小张移植10 000棵这种树苗,则可能成活9 000棵;④若小张移植20 000棵这种树苗,则一定成活18 000棵.其中合理的是( )
A、①③ B、①④ C、②③ D、②④8. 如图,点O为△ABC的外心,点I为△ABC的内心,若∠BIC=125°,则∠BOC的度数为( )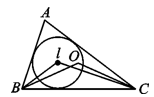 A、110° B、125° C、130° D、140°9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②a+b+c=2;③ ;④b>1.其中正确的结论个数是( )
A、110° B、125° C、130° D、140°9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②a+b+c=2;③ ;④b>1.其中正确的结论个数是( ) A、1个 B、2个 C、3个 D、4个10. 如图,在半径为6cm的⊙O中,点A是劣弧 的中点,点D是优弧 上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=3 cm;③扇形OCAB的面积为12π;④四边形ABOC是菱形.其中正确结论的序号是( )
A、1个 B、2个 C、3个 D、4个10. 如图,在半径为6cm的⊙O中,点A是劣弧 的中点,点D是优弧 上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=3 cm;③扇形OCAB的面积为12π;④四边形ABOC是菱形.其中正确结论的序号是( )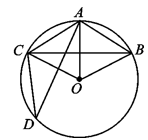 A、①③ B、①②③④ C、②③④ D、①③④
A、①③ B、①②③④ C、②③④ D、①③④二、填空题
-
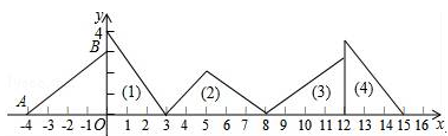
11. 边长为4的正六边形内接于 ,则 的半径是 .12. 在平面直角坐标系xOy中,若点B与点A(-2,3) 关于点O中心对称,则点B 的坐标为.13. 圆锥的底面半径是40cm,母线长90cm,它的侧面展开图的圆心角是°.14. 将抛物线y=2x2﹣12x+16绕它的顶点旋转180°,所得抛物线的解析式是.15. 如图,在平面直角坐标系中,已知点A(-4,0)、B(0,3),对△AOB连续作旋转变换依次得到三角形(1)、(2)、(3)、(4)、…,则第(2)个三角形的直角顶点的坐标是 , 第(2018)个三角形的直角顶点的坐标是 .
 16. 如图,在△ABC中,∠ACB=90°,D为边AB的中点,E、F分别为边AC、BC上的点,且AE=AD,BF=BD.若DE= ,DF=2则∠EDF=°,线段AB的长度=.
16. 如图,在△ABC中,∠ACB=90°,D为边AB的中点,E、F分别为边AC、BC上的点,且AE=AD,BF=BD.若DE= ,DF=2则∠EDF=°,线段AB的长度=.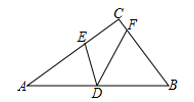
三、解答题
-
17. 已知m是方程 的一个根,求 的值.18. 如图,在平面直角坐标系中,△ABC的顶点为A(-3,-2),B(-5,3),C(0,4).
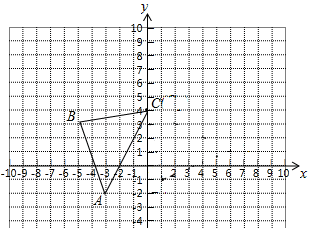
(1)、以C为旋转中心,将△ABC绕C逆时针旋转90°,画出旋转后的对应的△A1B1C1 , 写出点A1的坐标;(2)、求出(1)中点B旋转到点B1所经过的路径长(结果保留根号和π).19. 小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).(1)、如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .(2)、如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.(3)、从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)20. 关于 的一元二次方程 有两个不相等的实数根 .(1)、求实数m的取值范围;(2)、是否存在实数m,使得 成立?如果存在,求出m的值;如果不存在,请说明理由.21. 在平面直角坐标系xOy中,直线y=-x+2与反比例函数 (k≠0)的图象交于点A(-2,a)和点 . (1)、求反比例函数的表达式和点B的坐标;(2)、直接写出不等式 的解集.22. 已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,
(1)、求反比例函数的表达式和点B的坐标;(2)、直接写出不等式 的解集.22. 已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,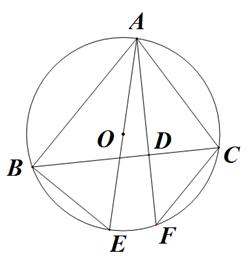 (1)、求证:AE是⊙O的直径;(2)、若∠ABC=∠EAC,AE=8,求AC的长.23. 农华公司以10元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
(1)、求证:AE是⊙O的直径;(2)、若∠ABC=∠EAC,AE=8,求AC的长.23. 农华公司以10元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:销售价格x(元/千克)
10
15
20
25
30
日销售量p(千克)
300
225
150
75
0
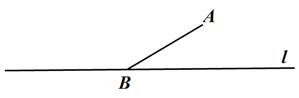
(1)、请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;(2)、农华公司应该如何确定这批农产品的销售价格,才能使日销售利润W元最大?(3)、若农华公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当20≤x≤25时,农经公司的日获利Q元的最大值为1215元,求a的值.(日获利=日销售利润-日支出费用)24.(1)、尺规作图:已知:如图,线段AB和直线 且点B在直线 上
求作:点C,使点C在直线 上并且使△ABC为等腰三角形.
作图要求:保留作图痕迹,不写作法,做出所有符合条件的点C.
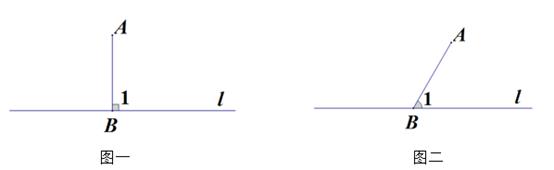
 (2)、特例思考:
(2)、特例思考:如图一,当∠1=90°时,符合(1)中条件的点C有个;
如图二,当∠1=60°时,符合(1)中条件的点C有个.
 (3)、拓展应用:
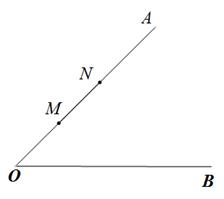
(3)、拓展应用:如图,∠AOB=45°,点M,N在射线OA上,OM=x,ON=x+2,点P是射线OB上的点.若使点P,M,N构成等腰三角形的点P有且只有三个,求x的值。