浙江省台州市椒江区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、选择题
-
1. 国家宝藏 节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多观众走进博物馆,让一个个馆藏文物鲜活起来 下面四幅图是我国一些博物馆的标志,其中是轴对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 若分式 在实数范围内有意义,则x的取值范围是A、
2. 若分式 在实数范围内有意义,则x的取值范围是A、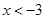 B、
B、 C、
C、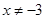 D、
D、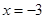 3. 的结果是A、0 B、
3. 的结果是A、0 B、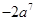 C、
C、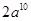 D、
D、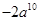 4. 下列分式中,最简分式是A、
4. 下列分式中,最简分式是A、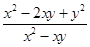 B、
B、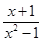 C、
C、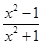 D、
D、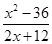 5. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线 ,另一把直尺压住射线 并且与第一把直尺交于点 ,小明说:“射线 就是 的角平分线 ”他这样做的依据是
5. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线 ,另一把直尺压住射线 并且与第一把直尺交于点 ,小明说:“射线 就是 的角平分线 ”他这样做的依据是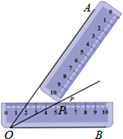 A、角平分线上的点到这个角两边的距离相等 B、角的内部到角的两边的距离相等的点在角的平分线上 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确6. 已知a、b、c为△ 的三边,且满足 ,则△ 是A、直角三角形 B、等边三角形 C、等腰三角形 D、不能确定7. 用直角三角板,作△ 的高,下列作法正确的是A、
A、角平分线上的点到这个角两边的距离相等 B、角的内部到角的两边的距离相等的点在角的平分线上 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确6. 已知a、b、c为△ 的三边,且满足 ,则△ 是A、直角三角形 B、等边三角形 C、等腰三角形 D、不能确定7. 用直角三角板,作△ 的高,下列作法正确的是A、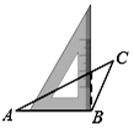 B、
B、 C、
C、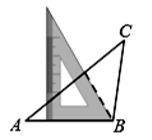 D、
D、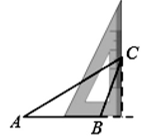 8. 如图,等腰△ 中, ,MN是边BC上一条运动的线段点M不与点B重合,点N不与点C重合 ,且 , 交AB于点D, 交AC于点E,在MN从左至右的运动过程中,△ 和△ 的面积之和
8. 如图,等腰△ 中, ,MN是边BC上一条运动的线段点M不与点B重合,点N不与点C重合 ,且 , 交AB于点D, 交AC于点E,在MN从左至右的运动过程中,△ 和△ 的面积之和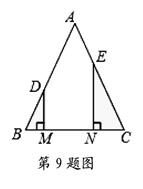 A、保持不变 B、先变小后变大 C、先变大后变小 D、一直变大9. 如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F,作CM⊥AD,垂足为M,下列结论不正确的是( )
A、保持不变 B、先变小后变大 C、先变大后变小 D、一直变大9. 如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F,作CM⊥AD,垂足为M,下列结论不正确的是( )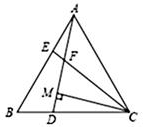 A、AD=CE B、 MF=
A、AD=CE B、 MF=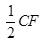 C、∠BEC=∠CDA
D、AM=CM
C、∠BEC=∠CDA
D、AM=CM
二、填空题
-
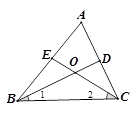
10. 用科学记数法表示0.0004=11. 因式分解: .12. 如图,在△ABC中,BD和CE是△ABC的两条角平分线,若∠A=52∘,则∠1+∠2的度数为 .
 13. 若正多边形的内角和是外角和的3倍,则这个正多边形的边数是 .14. 在如图所示的 方格中,连接格点AB、AC,则 度
13. 若正多边形的内角和是外角和的3倍,则这个正多边形的边数是 .14. 在如图所示的 方格中,连接格点AB、AC,则 度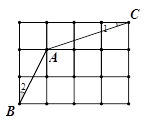 15. 如图,在等腰直角△ABC中,AB=4,点D在边AC上一点且AD=1,点E是AB边上一点,连接DE,以线段DE为直角边作等腰直角△DEF( D、E、F三点依次呈逆时针方向),当点F恰好落在BC边上时,则AE的长是 .
15. 如图,在等腰直角△ABC中,AB=4,点D在边AC上一点且AD=1,点E是AB边上一点,连接DE,以线段DE为直角边作等腰直角△DEF( D、E、F三点依次呈逆时针方向),当点F恰好落在BC边上时,则AE的长是 .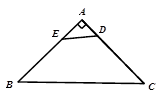
三、解答题
-
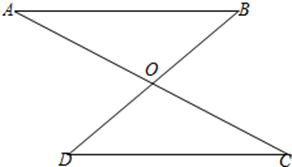
16. 计算(1)、(2)、(3)、17. 解方程18. 如图, , ,AC与BD相交于点 求证: .
 19. 如图,在△ 中, ,BC的垂直平分线交BC于E,交AC于D,且
19. 如图,在△ 中, ,BC的垂直平分线交BC于E,交AC于D,且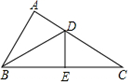 (1)、求证: ;(2)、求 的度数20. 某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用6000元购进电冰箱的数量与用4800元购进空调的数量相等.(1)、求每台电冰箱与空调的进价分别是多少?(2)、已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,现有两种进货方案①冰箱30台,空调70台;②冰箱50台,空调50台,那么该商店要获得最大利润应如何进货?21. 请按要求完成下面三道小题.
(1)、求证: ;(2)、求 的度数20. 某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用6000元购进电冰箱的数量与用4800元购进空调的数量相等.(1)、求每台电冰箱与空调的进价分别是多少?(2)、已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,现有两种进货方案①冰箱30台,空调70台;②冰箱50台,空调50台,那么该商店要获得最大利润应如何进货?21. 请按要求完成下面三道小题.
(1)、如图1,∠BAC关于某条直线对称吗?如果是,请画出对称轴 尺规作图,保留作图痕迹 ;如果不是,请说明理由.
(2)、如图2,已知线段AB和点C(A与C是对称点).
求作线段 ,使它与AB成轴对称,标明对称轴b,操作如下:连接AC; 作线段AC的垂直平分线,即为对称轴b;
作点B关于直线b的对称点D; 连接CD即为所求.
(3)、如图3,任意位置的两条线段AB,CD,且 (A与C是对称点).你能通过对其中一条线段作有限次的轴对称使它们重合吗?如果能,请描述操作方法或画出对称轴 尺规作图,保留作图痕迹 ;如果不能,请说明理由.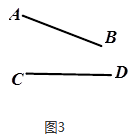
22. 如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”.(1)、下列分式: ; ; ; 其中是“和谐分式”是 填写序号即可 ;(2)、若a为正整数,且 为“和谐分式”,请写出所有满足条件的a值;(3)、在化简 时,小东和小强分别进行了如下三步变形:
小东:
小强:
显然,小强利用了其中的和谐分式,第三步所得结果比小东的结果简单,原因是: , 请你接着小强的方法完成化简.
23. 如图,在等边△ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E(点E不与点A重合).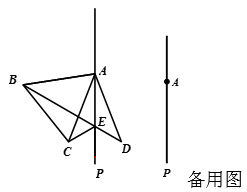 (1)、若∠CAP=20°.
(1)、若∠CAP=20°.①求∠AEB=°;
②连结CE,直接写出AE,BE,CE之间的数量关系 .
(2)、若∠CAP= (0º< <120º).①∠AEB的度数是否发生变化,若发生变化,请求出∠AEB度数;
②AE,BE,CE之间的数量关系是否发生变化,并证明你的结论.