山东省济宁市鱼台县2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、选择题
-
1. 如果3a=2b(ab≠0),那么下列比例式中正确的是( )
A、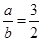 B、
B、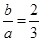 C、
C、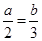 D、
D、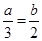 2. 如图,已知点P为反比例函数y=- 上一点,过点P向坐标轴引垂线,垂足分别为M,N,那么四边形MONP的面积为( )
2. 如图,已知点P为反比例函数y=- 上一点,过点P向坐标轴引垂线,垂足分别为M,N,那么四边形MONP的面积为( )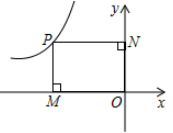 A、-6 B、6 C、3 D、123. 若将抛物线y=- x2先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是( )A、
A、-6 B、6 C、3 D、123. 若将抛物线y=- x2先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是( )A、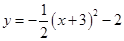 B、
B、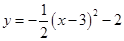 C、
C、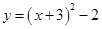 D、
D、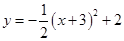 4. 若1- 是关于x的方程x2-2x+c=0的一个根,则c的值为( )A、-2 B、4 -2 C、3- D、1+5. 下列事件中,是必然事件的是( )A、掷一枚质地均匀的硬币,一定正面向上 B、车辆随机到达一个路口,遇到红灯 C、如果a2=b2 , 那么a=b D、将花生油滴在水中,油会浮在水面上6. △DEF和△ABC是位似图形,点O是位似中心,点D,E,F分别是OA,OB,OC的中点,若△DEF的面积是2,则△ABC的面积是( )
4. 若1- 是关于x的方程x2-2x+c=0的一个根,则c的值为( )A、-2 B、4 -2 C、3- D、1+5. 下列事件中,是必然事件的是( )A、掷一枚质地均匀的硬币,一定正面向上 B、车辆随机到达一个路口,遇到红灯 C、如果a2=b2 , 那么a=b D、将花生油滴在水中,油会浮在水面上6. △DEF和△ABC是位似图形,点O是位似中心,点D,E,F分别是OA,OB,OC的中点,若△DEF的面积是2,则△ABC的面积是( )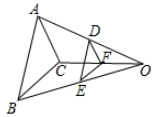 A、2 B、4 C、6 D、87. 如图,△ABC内接于⊙O,连结OA,OB,∠ABO=40。则∠C的度数是( )
A、2 B、4 C、6 D、87. 如图,△ABC内接于⊙O,连结OA,OB,∠ABO=40。则∠C的度数是( )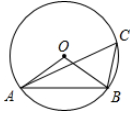 A、100° B、80° C、50° D、40°8. 设x1 , x2是方程x2-4x+m=0的两个根,且x1+x2-x1x2=1,那么m的值为( )A、2 B、-3 C、3 D、-29. 如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
A、100° B、80° C、50° D、40°8. 设x1 , x2是方程x2-4x+m=0的两个根,且x1+x2-x1x2=1,那么m的值为( )A、2 B、-3 C、3 D、-29. 如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )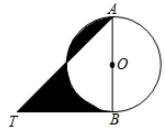 A、2 B、1 C、
A、2 B、1 C、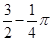 D、
D、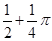 10. 小明以二次函数y=2x2-4x+8的图象为灵感为“某国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若AB=4,加DE=3,则杯子的高CE为( )
10. 小明以二次函数y=2x2-4x+8的图象为灵感为“某国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若AB=4,加DE=3,则杯子的高CE为( )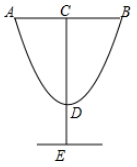 A、14 B、11 C、6 D、3
A、14 B、11 C、6 D、3二、填空题
-
11. 请你写出一个顶点在 轴上的二次函数表达式.
12. 已知反比例函数y = ,当x>0时,y随x的增大而增大,则m的取值范围是13. 如图,在矩形ABCD中,AB=5,AD=3.矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB’C’D’.若点B的对应点B’落在边CD上,则B’C的长为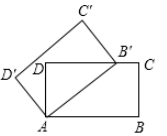 14. 若关于x的一元二次方程(k-1)x2+4x+1=0有实数根,则k的取值范围是15. 如图,点0为正六边形ABCDEF的中心,点M为AF中点,以点0为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2 , 则r1:r2=
14. 若关于x的一元二次方程(k-1)x2+4x+1=0有实数根,则k的取值范围是15. 如图,点0为正六边形ABCDEF的中心,点M为AF中点,以点0为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2 , 则r1:r2=
三、解答题:
-
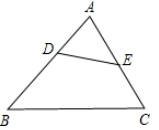
16. 如图,已知D,E分别是△ABC的边AB,AC上的点,且∠ADE=∠C.求证:AD·AB=AE·AC.
 17. 如图,在平面直角坐标系xOy中,点A(3,3),点B(4,0),点C(0,-1).
17. 如图,在平面直角坐标系xOy中,点A(3,3),点B(4,0),点C(0,-1).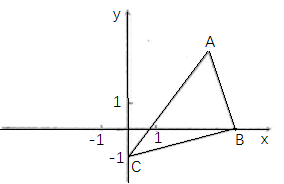 (1)、以点C为中心,把△ABC逆时针旋转90°,画出旋转后的图形△A’B’C’(要求尺规作图,不写作法,保留作图痕迹);(2)、在(1)的条件下,
(1)、以点C为中心,把△ABC逆时针旋转90°,画出旋转后的图形△A’B’C’(要求尺规作图,不写作法,保留作图痕迹);(2)、在(1)的条件下,①点A经过的路径AA’的长为;(结果保留 )
②写出B’的坐标为 .
18. 如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.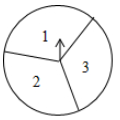 (1)、小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为;(2)、小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)19. 如图,一次函数y=x+4的图象与反比例函数y= (k为常数且k≠o)的图象交于A(-1,a),B两点,与x轴交于点C.
(1)、小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为;(2)、小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)19. 如图,一次函数y=x+4的图象与反比例函数y= (k为常数且k≠o)的图象交于A(-1,a),B两点,与x轴交于点C.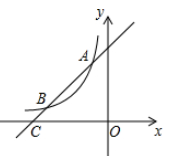 (1)、求此反比例函数的表达式;(2)、若点P在x轴上,且S△ACP= S△BOC,求点P的坐标.20. 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点O是AB边上一点,以O为圆心作⊙O,且经过A,D两点,交AB于点E·
(1)、求此反比例函数的表达式;(2)、若点P在x轴上,且S△ACP= S△BOC,求点P的坐标.20. 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点O是AB边上一点,以O为圆心作⊙O,且经过A,D两点,交AB于点E·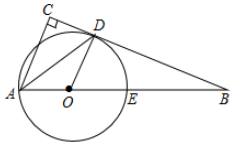 (1)、求证:BC是⊙O的切线;(2)、AC=2,AB=6,求BE的长.21. 阅读材料:各类方程的解法.
(1)、求证:BC是⊙O的切线;(2)、AC=2,AB=6,求BE的长.21. 阅读材料:各类方程的解法.求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式,求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组。求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验·各类方程附解法不尽相同,但是它们有一个共同的基本数学思想:转化,把未知转化为已知,用“转化,的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
 (1)、问题:方程x3+x2-2x=0的解是x1=0,x2= , x3=;(2)、拓展:用“转化”思想求方程 的解;(3)、应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C,求AP的长.22. 在平面直角坐标系xOy中(如图).已知抛物线y=- x2+bx+c经过点A(-1,0)和点B(0, ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)、问题:方程x3+x2-2x=0的解是x1=0,x2= , x3=;(2)、拓展:用“转化”思想求方程 的解;(3)、应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C,求AP的长.22. 在平面直角坐标系xOy中(如图).已知抛物线y=- x2+bx+c经过点A(-1,0)和点B(0, ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.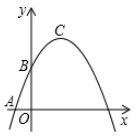 (1)、求这条抛物线的表达式;(2)、求线段CD的长;(3)、将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.
(1)、求这条抛物线的表达式;(2)、求线段CD的长;(3)、将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.