2018-2019学年初中数学北师大版七年级下册第一章 整式的乘除 达标检测卷
试卷更新日期：2019-01-24 类型：同步测试
一、选择题
-
1. 计算(－x2y)3的结果是（ ）A、x6y3 B、x5y3 C、－x6y3 D、－x2y32. 下列运算正确的是（ ）A、x2＋x2＝x4 B、(a－b)2＝a2－b2 C、(－a2)3＝－a6 D、3a2·2a3＝6a63. 花粉的质量很小，一粒某种植物花粉的质量约为0.000 037 mg，已知1 g＝1 000 mg，那么0.000 037 mg用科学记数法表示为（ ）A、3.7×10－5 g B、3.7×10－6 g C、3.7×10－7 g D、3.7×10－8 g4. 在下列计算中，不能用平方差公式计算的是（ ）A、(m－n)(－m＋n) B、
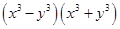C、(－a－b)(a－b)
D、
5. 已知a+b=m，ab=－4，化简(a－2)(b－2)的结果是( )A、6 B、2m－8 C、2m D、－2m6. 若3x＝4，9y＝7，则3x－2y的值为（ ）A、
B、
C、－3
D、
7. 如果x＋m与x＋3的乘积中不含x的一次项，则m的值为（ ）A、－3 B、3 C、0 D、18. 若a＝－0.32 ， b＝(－3)－2 ， c＝ ，d＝ ，则（ ）A、a＜b＜c＜d B、a＜b＜d＜c C、a＜d＜c＜b D、c＜a＜d＜b9. 如图，从边长为 cm的正方形纸片中剪去一个边长为 cm的正方形( ＞0)，剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙)，则长方形的面积为（ ）
A、 B、 C、 D、10. 若A＝(2＋1)(22＋1)(24＋1)(28＋1)＋1，则A的末位数字是（ ）A、2 B、4 C、6 D、8二、填空题
-
11. 计算：(2a)3·(－3a2)＝ ．12. 若x＋y＝5，x－y＝1，则式子x2－y2的值是 ．13. 计算：(－2)2 016＋(－2)2 017＝ ．14. 若(a2－1)0＝1，则a的取值范围是 ．15. 已知(x＋y)2＝1，(x－y)2＝49，则x2＋y2的值为 ．16. 已知x2－x－1＝0，则代数式－x3＋2x2＋2 018的值为 ．17. 如果 ＝63，那么a＋b的值为 ．18. 已知a＋ ＝5，则a2＋ 的结果是 ．
三、解答题
-
19. 计算：(1)、－23＋ (2 018＋3)0－ ；(2)、992－69×71；(3)、 ÷(－3xy);(4)、(－2＋x)(－2－x)；(5)、(a＋b－c)(a－b＋c);(6)、(3x－2y＋1)2.20. 先化简，再求值：
[(x2＋y2)－(x＋y)2＋2x(x－y)]÷4x，其中x－2y＝2.
21.(1)、已知a＋b＝7，ab＝12.求下列各式的值：①a2－ab＋b2；②(a－b)2.
(2)、已知a＝275 ， b＝450 ， c＝826 ， d＝1615 ， 比较a，b，c，d的大小．22. 先阅读再解答：我们已经知道，根据几何图形的面积关系可以说明完全平方公式，实际上还有一些等式也可以用这种方式加以说明，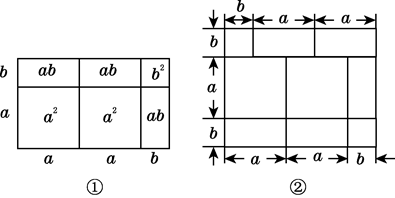
例如：
(2a＋b)(a＋b)＝2a2＋3ab＋b2 ， 就可以用图①的面积关系来说明．
(1)、根据图②写出一个等式：；(2)、已知等式：(x＋p)(x＋q)＝x2＋(p＋q)x＋pq，请你画出一个相应的几何图形加以说明．23. 已知(x2＋px＋8)(x2－3x＋q)的展开式中不含x2和x3项，求p，q的值．24. 王老师家买了一套新房，其结构如图所示(单位：m)．他打算将卧室铺上木地板，其余部分铺上地砖．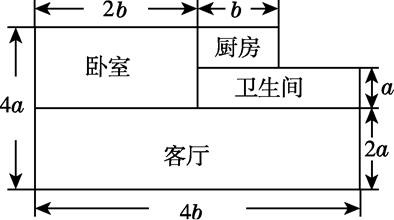
(1)、木地板和地砖分别需要多少平方米？(2)、如果地砖的价格为每平方米x元，木地板的价格为每平方米3x元，那么王老师需要花多少钱？25. 利用我们学过的知识，可以导出下面这个形式优美的等式：a2＋b2＋c2－ab－bc－ac＝ [(a－b)2＋(b－c)2＋(c－a)2]，
该等式从左到右的变形，不仅保持了结构的对称性，还体现了数学的和谐、简洁美．
(1)、请你检验这个等式的正确性；(2)、若a＝2 016，b＝2 017，c＝2 018，你能很快求出a2＋b2＋c2－ab－bc－ac的值吗？26. 探索：(x－1)(x＋1)＝x2－1； (x－1)(x2＋x＋1)＝x3－1；
(x－1)(x3＋x2＋x＋1)＝x4－1； (x－1)(x4＋x3＋x2＋x＋1)＝x5－1；
…
(1)、试写出第五个等式；(2)、试求26＋25＋24＋23＋22＋2＋1的值；(3)、判断22 017＋22 016＋22 015＋…＋22＋2＋1的值的个位数字是几．