浙江省湖州市长兴县2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-01-24 类型:期末考试
一、选择题
-
1. 下列事件中,必然事件是( )A、掷一枚硬币,着地时反面向上. B、星期天一定是晴天 C、打开电视机,正在播放动画片. D、在标准大气压下,水加热到100℃会沸腾2. 已知 ,则 的值是( )
A、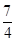 B、
C、
D、
B、
C、
D、 3. 把抛物线y=x2向右平移1个单位,所得抛物线的函数表达式为 ( )A、y=x2+1 B、y=(x+1)2 C、y=x2-1 D、y=(x-1)24. 一个不透明的布袋里装有7个球,其中3个红球,4个白球,它们除颜色外都相同,从布袋中随机摸出一个球,摸出的球是红球的概率是( )A、
3. 把抛物线y=x2向右平移1个单位,所得抛物线的函数表达式为 ( )A、y=x2+1 B、y=(x+1)2 C、y=x2-1 D、y=(x-1)24. 一个不透明的布袋里装有7个球,其中3个红球,4个白球,它们除颜色外都相同,从布袋中随机摸出一个球,摸出的球是红球的概率是( )A、 B、
B、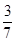 C、
D、
5. 如图,PA,PB分别切⊙O于点A,曰,PA=12,CD切⊙O于点E,交削,PB于点C,D两点,则△PCD的周长是( )
C、
D、
5. 如图,PA,PB分别切⊙O于点A,曰,PA=12,CD切⊙O于点E,交削,PB于点C,D两点,则△PCD的周长是( )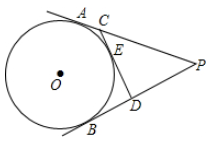 A、12 B、18 C、24 D、306. 如图,圆拱桥的拱顶到水面的距离CD为8m,水面宽AB为8m,则桥拱半径OC的长是( )
A、12 B、18 C、24 D、306. 如图,圆拱桥的拱顶到水面的距离CD为8m,水面宽AB为8m,则桥拱半径OC的长是( ) A、4m B、5m C、6m D、8m7. 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以点C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A、4m B、5m C、6m D、8m7. 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以点C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( ) A、(6,5) B、(6,0) C、(6,4) D、(4,2)8. 在△ABC中,AB=12 ,AC=13,cosB= ,则BC的边长为( )A、7 B、8 C、8或17 D、7或179. 超市有一种”喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,轴截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,这个包装盒的长AD(不计重合部分,两个果冻之间没有挤压)至少为( )
A、(6,5) B、(6,0) C、(6,4) D、(4,2)8. 在△ABC中,AB=12 ,AC=13,cosB= ,则BC的边长为( )A、7 B、8 C、8或17 D、7或179. 超市有一种”喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,轴截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,这个包装盒的长AD(不计重合部分,两个果冻之间没有挤压)至少为( )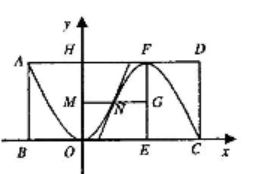 A、(6+3 )cm B、(6+2 )cm C、(6+2 )cm D、(6+3 )cm10. 已知AD,BE,CF分别为△ABC的三条高,连结DE,DF, ∠ABC=45°,∠ACB=60° ,则 的值是( )
A、(6+3 )cm B、(6+2 )cm C、(6+2 )cm D、(6+3 )cm10. 已知AD,BE,CF分别为△ABC的三条高,连结DE,DF, ∠ABC=45°,∠ACB=60° ,则 的值是( )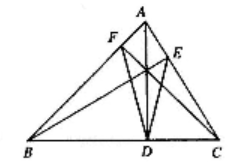 A、 B、
A、 B、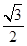 C、
C、 D、
D、
二、填空题
-
11. 已知线段AB=6cm,点C是线段AB的黄金分割点(AC>BC),则AC的长为 cm12. 某人在坡比为1: 的斜坡上前进了10米,则他所在的位置比原来升高了米13. 如图,在⊙O中, , ∠AOB=40°,点D在⊙O上,连结CD,AD,则 ∠ADC 的度数是
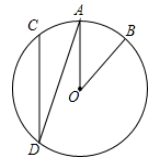 14. 如图,把△ABC沿AB边平移到△A’B’C’的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半.若AB= ,则此三角形平移的距离AA’是 .
14. 如图,把△ABC沿AB边平移到△A’B’C’的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半.若AB= ,则此三角形平移的距离AA’是 .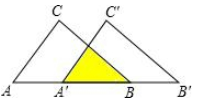 15. 已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而减小,且-4≤x≤1时,y的最大值为7,则a的值为16. 如图,在Rt△ABC中,∠BCA=90°,∠A=30°,AB=4 .若动点D在线段AC上(不与点A,C重合),过点D作DE上AC交AB边于点E若点A关于点D的对称点为点F,以FC为半径作⊙C,当DE= 时,⊙C与直线AB相切.
15. 已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而减小,且-4≤x≤1时,y的最大值为7,则a的值为16. 如图,在Rt△ABC中,∠BCA=90°,∠A=30°,AB=4 .若动点D在线段AC上(不与点A,C重合),过点D作DE上AC交AB边于点E若点A关于点D的对称点为点F,以FC为半径作⊙C,当DE= 时,⊙C与直线AB相切.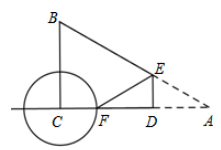
三、解答题
-
17. 计算:4sin260°+tan45°-2sin30°18. 已知:如图,△ABC中,AD是角平分线,点E在AC上,∠ADE=∠B
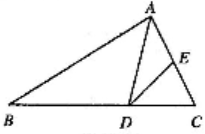
求证:AD2=AE·AB
19. 已知抛物线的顶点坐标为(-1,2),且过点(1,0)(1)、求抛物线的函数表达式;(2)、求抛物线与坐标轴的交点坐标20. 如图是某货站传送货物的平面示意图为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°,已知原传送带AB长为3 米.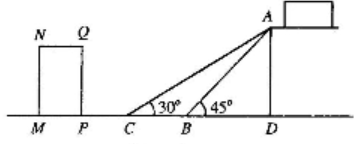 (1)、求新传送带AC的长度;(2)、如果需要在货物着地点C的左侧留出2.5米的通道,请判断距离B点5米的货物MNQP是否需要挪走,并说明理由.(参考数据: ≈1.4 ≈1.7)21. 为弘扬中华优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《大学》,《中庸》(依次用字母A,B,C表示这三个材料),将A,B,C分别写在3张完全相同的不透明卡片的正面上,背面朝上洗匀后放在桌面上,比赛时小礼先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由小智从中随机抽取一张卡片,他俩按各自抽取的内容进行诵读比赛(1)、小礼诵读《论语》的概率是;(直接写出答案)(2)、请用列表或画树状图的方法求他俩诵读两个不同材料的概率.22. 如图,在△ABC中,BE是它的角平分线,∠C=90°,点D在AB边上,以DB为直径的半圆O经过点E,交BC于点F
(1)、求新传送带AC的长度;(2)、如果需要在货物着地点C的左侧留出2.5米的通道,请判断距离B点5米的货物MNQP是否需要挪走,并说明理由.(参考数据: ≈1.4 ≈1.7)21. 为弘扬中华优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《大学》,《中庸》(依次用字母A,B,C表示这三个材料),将A,B,C分别写在3张完全相同的不透明卡片的正面上,背面朝上洗匀后放在桌面上,比赛时小礼先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由小智从中随机抽取一张卡片,他俩按各自抽取的内容进行诵读比赛(1)、小礼诵读《论语》的概率是;(直接写出答案)(2)、请用列表或画树状图的方法求他俩诵读两个不同材料的概率.22. 如图,在△ABC中,BE是它的角平分线,∠C=90°,点D在AB边上,以DB为直径的半圆O经过点E,交BC于点F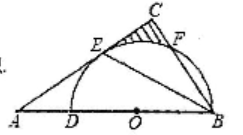 (1)、求证:AC是⊙O的切线;(2)、已知sinA= ,⊙O的半径为3,求图中阴影部分的面积23. 定义:有—个角是其对角两倍的圆的内接四边形叫做圆美四边形,其中这个角叫做美角,已知四边形ABCD是圆美四边形.
(1)、求证:AC是⊙O的切线;(2)、已知sinA= ,⊙O的半径为3,求图中阴影部分的面积23. 定义:有—个角是其对角两倍的圆的内接四边形叫做圆美四边形,其中这个角叫做美角,已知四边形ABCD是圆美四边形.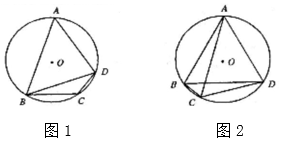 (1)、求美角∠C的度数;(2)、如图1,若⊙O的半径为2 ,求BD的长;(3)、如图2,若CA平分∠BCD,求证:BC+CD=AC24. 如图,已知抛物线 (k为常数,且k>o)与x轴从左至右依次交于A,B两点,与y轴交于点C,过点B的直线 与抛物线的另一交点为D.
(1)、求美角∠C的度数;(2)、如图1,若⊙O的半径为2 ,求BD的长;(3)、如图2,若CA平分∠BCD,求证:BC+CD=AC24. 如图,已知抛物线 (k为常数,且k>o)与x轴从左至右依次交于A,B两点,与y轴交于点C,过点B的直线 与抛物线的另一交点为D. (1)、若点D的横坐标为-5,求抛物线的函数表达式;(2)、过D点向x轴作垂线,垂足为点M,连结AD,若∠MDA=∠ABD,求点D的坐标;(3)、若在第一象限的抛物线上有一点P,使得以点A,B,P为顶点的三角形与△ABC相似,请直接写出△ABC的面积
(1)、若点D的横坐标为-5,求抛物线的函数表达式;(2)、过D点向x轴作垂线,垂足为点M,连结AD,若∠MDA=∠ABD,求点D的坐标;(3)、若在第一象限的抛物线上有一点P,使得以点A,B,P为顶点的三角形与△ABC相似,请直接写出△ABC的面积