湖北省襄阳老河口市2017-2018学年八年级上学期数学期中考试试卷
试卷更新日期:2019-01-23 类型:期中考试
一、单选题
-
1. 等腰三角形的两边长分别为5cm,4cm,则它的周长是( )A、14cm B、13cm C、16cm或9cm D、13cm或14cm2. 一个多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数是( )A、6条 B、7条 C、8条 D、9条3. 如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠B′DC等于( )
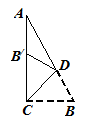 A、40° B、60° C、70° D、80°4. 如图所示,八年级某同学书上的图形(三角形)不小心被墨迹污染了一部分,但他很快就根据所学知识,画出一个与书上完全一样的三角形,那么这两个三角形全等的依据是( )
A、40° B、60° C、70° D、80°4. 如图所示,八年级某同学书上的图形(三角形)不小心被墨迹污染了一部分,但他很快就根据所学知识,画出一个与书上完全一样的三角形,那么这两个三角形全等的依据是( ) A、SSS B、SAS C、AAS D、ASA5. 点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,则下列不符合题意的是( )A、PQ>5 B、PQ≥5 C、PQ<5 D、PQ≤56. △ABC是一个任意三角形,用直尺和圆规作出∠A,∠B的平分线,如果两条平分线交于点O,那么下列选项中不正确的是( )A、点O一定在△ABC的内部 B、点O到△ABC的三边距离一定相等 C、∠C的平分线一定经过点O D、点O到△ABC三顶点的距离一定相等7. 如图,点D,E分别在AB,AC上,AB=AC,∠B=∠C,若AD=2,BD=3,则CE的长为( )
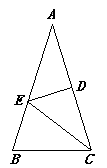
A、SSS B、SAS C、AAS D、ASA5. 点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,则下列不符合题意的是( )A、PQ>5 B、PQ≥5 C、PQ<5 D、PQ≤56. △ABC是一个任意三角形,用直尺和圆规作出∠A,∠B的平分线,如果两条平分线交于点O,那么下列选项中不正确的是( )A、点O一定在△ABC的内部 B、点O到△ABC的三边距离一定相等 C、∠C的平分线一定经过点O D、点O到△ABC三顶点的距离一定相等7. 如图,点D,E分别在AB,AC上,AB=AC,∠B=∠C,若AD=2,BD=3,则CE的长为( )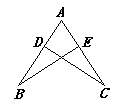 A、2 B、3 C、5 D、无法确定8. 点A(3,4)关于x轴对称的点的坐标为( )A、(-3,4) B、(4,3) C、(-3,-4) D、(3,-4)9. 已知∠AOB=30°,点P在∠AOB的内部,点P1与点P关于OB对称,点P2与点P关于OA对称,则以点P1 , O,P2为顶点的三角形是( )
A、2 B、3 C、5 D、无法确定8. 点A(3,4)关于x轴对称的点的坐标为( )A、(-3,4) B、(4,3) C、(-3,-4) D、(3,-4)9. 已知∠AOB=30°,点P在∠AOB的内部,点P1与点P关于OB对称,点P2与点P关于OA对称,则以点P1 , O,P2为顶点的三角形是( )
A、直角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形10. 如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=20°,则∠ACF的度数为( ) A、60° B、50° C、40° D、20°11. 如图,在△PAB中,PA=PB,M,N,K分别在PA,PB,AB上,且AM=BK,BN=AK,若∠MKN=40°,则∠P的度数为( )
A、60° B、50° C、40° D、20°11. 如图,在△PAB中,PA=PB,M,N,K分别在PA,PB,AB上,且AM=BK,BN=AK,若∠MKN=40°,则∠P的度数为( )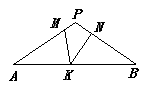 A、140° B、90° C、100° D、110°
A、140° B、90° C、100° D、110°二、填空题
-
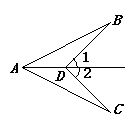
12. 若一个三角形的三个内角度数之比为4∶3∶2,则这个三角形的最大内角为度.13. 如图,∠1=∠2,要使△ABD≌△ACD,还需添加一个条件是: . (填上你认为适当的一个条件即可)
 14. 超重机的底座、输电线路的支架、自行车的斜支架等,都是采用三角形结构,这样做的数学道理是利用了 .15. 如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为 .
14. 超重机的底座、输电线路的支架、自行车的斜支架等,都是采用三角形结构,这样做的数学道理是利用了 .15. 如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为 .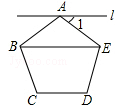
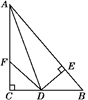
16. 等腰三角形的一个外角为80°,则它的底角为度.17. 如图,在△ABC中,D在边AC上,如果AB=BD=DC,且∠C=40°,那么∠A=°.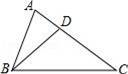 18. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD= .
18. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD= .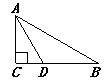 19. (题文)如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE=cm .
19. (题文)如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE=cm .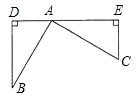 20. 如图,△ABC是等边三角形,点D,E分别是BC,AC边上的点,且CD=AE,AD,BE交于点F,延长AD至点P,使PF=BF,连接BP,CP,若BP=5,CP=3,则AP的长为 .
20. 如图,△ABC是等边三角形,点D,E分别是BC,AC边上的点,且CD=AE,AD,BE交于点F,延长AD至点P,使PF=BF,连接BP,CP,若BP=5,CP=3,则AP的长为 .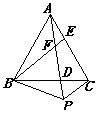
三、解答题
-
21. 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则△ABP周长的最小值是 .
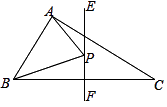 22. 如图,在△ABC中,∠C=60°,△ABC的高AD,BE相交于点F.求∠AFB的度数.
22. 如图,在△ABC中,∠C=60°,△ABC的高AD,BE相交于点F.求∠AFB的度数.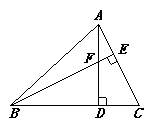 23. 如图,请按下列要求用尺规作图,不写作法,但要保留痕迹:
23. 如图,请按下列要求用尺规作图,不写作法,但要保留痕迹: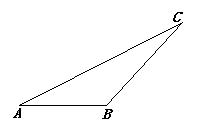 (1)、作出△ABC的角平分线CD;(2)、作出△ABC的高AE.24. 如图,CE=CB,CD=CA,∠DCA=∠ECB,求证:DE=AB.
(1)、作出△ABC的角平分线CD;(2)、作出△ABC的高AE.24. 如图,CE=CB,CD=CA,∠DCA=∠ECB,求证:DE=AB. 25. 如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.
25. 如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.求证:AD=AE.
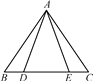 26. 如图,在四边形ABCD中, ∠B=∠D=90°,∠DAB与∠DCB 的平分线分别交DC,AB于E,F.求证:AE∥CF.
26. 如图,在四边形ABCD中, ∠B=∠D=90°,∠DAB与∠DCB 的平分线分别交DC,AB于E,F.求证:AE∥CF. 27. 如图18,在△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,若AD=1,求BC的长.
27. 如图18,在△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,若AD=1,求BC的长.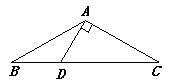 28. 如图19,在△ABC中,AB=AC,AC的垂直平分线交AB于E,D为垂足,连接EC.若BC=EC,求∠BED的度数.
28. 如图19,在△ABC中,AB=AC,AC的垂直平分线交AB于E,D为垂足,连接EC.若BC=EC,求∠BED的度数.