河南省郑州市2018届九年级上学期数学期中考试试卷
试卷更新日期:2019-01-23 类型:期中考试
一、单选题
-
1. 下列根式中,不能与 合并的是( )A、
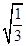 B、
B、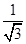 C、
C、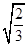 D、
D、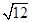 2. 如果ab>0,a+b<0,那么下面各式:① ,② =1,③ ÷ =﹣b,其中正确的是( )A、①② B、②③ C、①③ D、①②③3. 对于任意的正数m,n定义运算※为:m※n= 计算(3※2)×(8※12)的结果为( )A、 2-4
2. 如果ab>0,a+b<0,那么下面各式:① ,② =1,③ ÷ =﹣b,其中正确的是( )A、①② B、②③ C、①③ D、①②③3. 对于任意的正数m,n定义运算※为:m※n= 计算(3※2)×(8※12)的结果为( )A、 2-4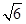 B、2
C、 2
D、20
4. 关于x的一元二次方程(m﹣2)x2+2x+1=0有实数根,则m的取值范围是( )
B、2
C、 2
D、20
4. 关于x的一元二次方程(m﹣2)x2+2x+1=0有实数根,则m的取值范围是( )
A、m≤3 B、m<3 C、m<3且m≠2 D、m≤3且m≠25. 关于x的一元二次方程x2﹣kx+2k﹣1=0的两个实数根分别是x1、x2 , 且x12+x22=7,则(x1﹣x2)2的值是( )A、13或11 B、12或﹣11 C、13 D、126. 三角形两边的长是3和4,第三边的长是方程x2﹣12x+35=0的根,则该三角形的周长为( )A、14 B、12 C、12或14 D、以上都不对7. 学校要组织足球比赛,赛制为单循环形式(每两队之间赛一场).计划安排21场比赛,应邀请多少个球队参赛?设邀请x个球队参赛.根据题意,下面所列方程正确的是( )A、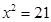 B、
B、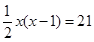 C、
C、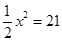 D、
D、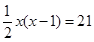 8. 某种衬衣的价格经过连续两次降价后,由每件150元降至96元,平均每次降价的百分率是( )A、10% B、20% C、30% D、40%9. 如图所示,已知PN∥BC,AD⊥BC交PN于点E,交BC于点D,若 = ,求 的值是( )
8. 某种衬衣的价格经过连续两次降价后,由每件150元降至96元,平均每次降价的百分率是( )A、10% B、20% C、30% D、40%9. 如图所示,已知PN∥BC,AD⊥BC交PN于点E,交BC于点D,若 = ,求 的值是( ) A、 B、
A、 B、 C、
C、 D、
10. 如图,在△ABC中,AD是BC边上的中线,E在AC边上,且AE:EC=1:2,BE交AD于P,则AP:PD等于( )
D、
10. 如图,在△ABC中,AD是BC边上的中线,E在AC边上,且AE:EC=1:2,BE交AD于P,则AP:PD等于( )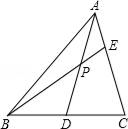 A、1:1 B、1:2 C、2:3 D、4:3
A、1:1 B、1:2 C、2:3 D、4:3二、填空题
-
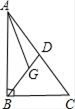
11. 若 ,则xy﹣3的值为 .12. 若(x2+y2﹣1)(x2+y2+1)=8,则x2+y2的值是 .13. 若 =3,当b+2d+3f=4时,则a+2c+3e= .14. 如图所示,已知点G为Rt△ABC的重心,∠ABC=90°,若AB=12cm,BC=9cm,则△AGD的面积是 .
 15. 如图所示,在平面直角坐标系中,OA1=1,将边长为1的正方形一边与x轴重合按图中规律摆放,其中每两个正方形的间距都是1,则点A2017的坐标为 .
15. 如图所示,在平面直角坐标系中,OA1=1,将边长为1的正方形一边与x轴重合按图中规律摆放,其中每两个正方形的间距都是1,则点A2017的坐标为 .
三、解答题
-
16. 解下列方程:(1)、(x+1)(x﹣1)+2(x+3)=13;(2)、2(y﹣4)2=y2﹣16.17. 已知α是锐角,且sin(α+15°)= ,计算: ﹣4cosα﹣(π﹣3.14)0+tanα+( )﹣1的值.18. 已知关于x的方程mx2﹣(m+2)x+2=0(m≠0).(1)、求证:方程总有两个实数根;(2)、若方程的两个实数根都是整数,求正整数m的值.
19. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).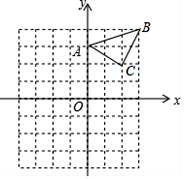 (1)、△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是;(2)、以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是;(画出图形)(3)、△A2B2C2的面积是平方单位.20. 如图,在△ABC中,DE∥BC,EF∥CD,求证:AD2=AF•AB.
(1)、△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是;(2)、以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是;(画出图形)(3)、△A2B2C2的面积是平方单位.20. 如图,在△ABC中,DE∥BC,EF∥CD,求证:AD2=AF•AB.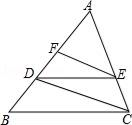 21. 某公司投资新建了一商场,共有商铺30间,据推测,当每间的年租金定为10万元时,可全部租出,若每间的年租金每增加5000元,少租出商铺1间,该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5000元.(1)、当每间商铺的年租金定为12万元时,能租出多少间?(2)、当每间商铺的年租金定为多少万元时,该公司的年收益为285万元?(收益=租金﹣各种费用)22. 如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么:
21. 某公司投资新建了一商场,共有商铺30间,据推测,当每间的年租金定为10万元时,可全部租出,若每间的年租金每增加5000元,少租出商铺1间,该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5000元.(1)、当每间商铺的年租金定为12万元时,能租出多少间?(2)、当每间商铺的年租金定为多少万元时,该公司的年收益为285万元?(收益=租金﹣各种费用)22. 如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么: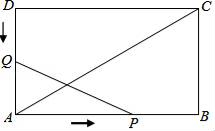 (1)、当t为何值时,△QAP是等腰直角三角形?(2)、当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?23. 请你认真阅读下面的小探究系列,完成所提出的问题.
(1)、当t为何值时,△QAP是等腰直角三角形?(2)、当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?23. 请你认真阅读下面的小探究系列,完成所提出的问题.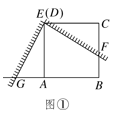

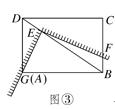 (1)、如图①,将角尺放在正方形ABCD上,使角尺的直角顶点E与正方形ABCD的顶点D重合,角尺的一边交CB于点F , 另一边交BA的延长线于点G.求证:EF=EG;(2)、如图②,移动角尺,使角尺的顶点E始终在正方形ABCD的对角线BD上,其余条件不变,请你思考后直接回答EF和EG的数量关系:EF=EG(填“=”或“≠”);(3)、运用(1)(2)解答中所积累的活动经验和数学知识,完成下题:如图③,将(2)中的“正方形ABCD”改成“矩形ABCD”,使角尺的一边经过点A(即点G、A重合),其余条件不变,若AB=4,DG=3,求 的值.
(1)、如图①,将角尺放在正方形ABCD上,使角尺的直角顶点E与正方形ABCD的顶点D重合,角尺的一边交CB于点F , 另一边交BA的延长线于点G.求证:EF=EG;(2)、如图②,移动角尺,使角尺的顶点E始终在正方形ABCD的对角线BD上,其余条件不变,请你思考后直接回答EF和EG的数量关系:EF=EG(填“=”或“≠”);(3)、运用(1)(2)解答中所积累的活动经验和数学知识,完成下题:如图③,将(2)中的“正方形ABCD”改成“矩形ABCD”,使角尺的一边经过点A(即点G、A重合),其余条件不变,若AB=4,DG=3,求 的值.