广西钦州市2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2019-01-23 类型:期末考试
一、单选题
-
1. 在以下四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列每组数分别表示三根小棒的长度,将它们首尾连接后,能摆成三角形的一组是( )A、1、2、3 B、2、3、5 C、2、3、6 D、3、5、73. 下列运算不正确的是 ( )
2. 下列每组数分别表示三根小棒的长度,将它们首尾连接后,能摆成三角形的一组是( )A、1、2、3 B、2、3、5 C、2、3、6 D、3、5、73. 下列运算不正确的是 ( )
A、x2x3=x5 B、(x2)4=x8 C、x3+x3=2x6 D、(-2x)3=-8x34. 生物界和医学界对病毒的研究从来没有停过脚步,最近科学家发现了一种病毒的长度约为0.00000456mm,则数据0.00000456用科学记数法表示为( )A、4.56×10﹣5 B、0.456×10﹣7 C、4.56×10﹣6 D、4.56×10﹣85. 要使分式 有意义,则x应满足的条件是( )A、x>﹣1 B、x<﹣1 C、x≠1 D、x≠﹣16. 在平面直角坐标系中,点P(-2,3)关于x轴的对称点在( ).A、第四象限 B、第三象限 C、第二象限 D、第一象限7. 如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( ) A、∠BCA=∠F B、∠B=∠E C、BC∥EF D、∠A=∠EDF8. 已知等腰△ABC的两条边长分别是5和6,则△ABC的周长为( )A、11 B、16 C、17 D、16或179. 下列等式从左到右的变形,属于因式分解的是( )A、a(x﹣y)=ax﹣ay B、x2﹣9+x=(x﹣3)(x+3)+x C、(x+1)(x+2)=x2+3x+2 D、x2y﹣y=(x﹣1)(x+1)y10.
A、∠BCA=∠F B、∠B=∠E C、BC∥EF D、∠A=∠EDF8. 已知等腰△ABC的两条边长分别是5和6,则△ABC的周长为( )A、11 B、16 C、17 D、16或179. 下列等式从左到右的变形,属于因式分解的是( )A、a(x﹣y)=ax﹣ay B、x2﹣9+x=(x﹣3)(x+3)+x C、(x+1)(x+2)=x2+3x+2 D、x2y﹣y=(x﹣1)(x+1)y10.用尺规作图法作已知角∠AOB的平分线的步骤如下:
①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;
②分别以点D,E为圆心,以大于 DE的长为半径作弧,两弧在∠AOB的内部相交于点C;
③作射线OC.
则射线OC为∠AOB的平分线.
由上述作法可得△OCD≌△OCE的依据是( )
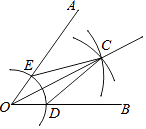 A、SAS B、ASA C、AAS D、SSS11. 甲、乙两个工程队进行污水管道整修,已知乙比甲每天多修3km,甲整修6km的工作时间与乙整修8km的工作时间相等,求甲、乙两个工程队每天分别整修污水管道多少km?设甲每天整修xkm,则可列方程为( )A、
A、SAS B、ASA C、AAS D、SSS11. 甲、乙两个工程队进行污水管道整修,已知乙比甲每天多修3km,甲整修6km的工作时间与乙整修8km的工作时间相等,求甲、乙两个工程队每天分别整修污水管道多少km?设甲每天整修xkm,则可列方程为( )A、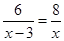 B、
B、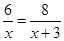 C、
C、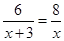 D、
D、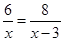 12. 如图,已知AC﹣BC=3,AB的垂直平分线分别交AB、AC于点D,E,△BCE的周长是15,则AC的长为( )
12. 如图,已知AC﹣BC=3,AB的垂直平分线分别交AB、AC于点D,E,△BCE的周长是15,则AC的长为( )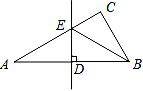 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9二、填空题
-
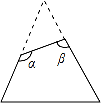
13. 计算:(a+1)(a﹣3)= .14. 钝角三角形三边上的中线的交点在此三角形(填写“内”或“外”或“边上”).15. 若分式 的值为0,则y= .16. 如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β= .
 17. 如图,点O在△ABC内,且到三边的距离相等,若∠A=60°,则∠BOC= .
17. 如图,点O在△ABC内,且到三边的距离相等,若∠A=60°,则∠BOC= .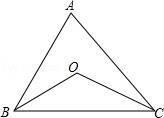 18. 先阅读后计算:为了计算4×(5+1)×(52+1)的值,小黄把4改写成5﹣1后,连续运用平方差公式得:
18. 先阅读后计算:为了计算4×(5+1)×(52+1)的值,小黄把4改写成5﹣1后,连续运用平方差公式得:4×(5+1)×(52+1)=(5﹣1)×(5+1)×(52+1)
=(52﹣1)×(52+1)=252﹣1=624.
请借鉴小黄的方法计算:
(1+ )×(1+ )×(1+ )×(1+ )×(1+ )×(1+ )×(1+ ),结果是 .
三、解答题
-
19.(1)、计算:(6x2﹣8xy)÷2x;(2)、分解因式:a3﹣6a2+9a.20. 如图,已知A(0,4)、B(﹣2,2)、C(3,0).
 (1)、作△ABC关于x轴对称的△A1B1C1 , 并写出点B的对应点B1的坐标;(2)、求△A1B1C1的面积S.21. 解分式方程: = ﹣2.22. 先化简再求值: (1- ),其中x= .23. 如图,已知AB=DC,AC=DB.求证:∠1=∠2.
(1)、作△ABC关于x轴对称的△A1B1C1 , 并写出点B的对应点B1的坐标;(2)、求△A1B1C1的面积S.21. 解分式方程: = ﹣2.22. 先化简再求值: (1- ),其中x= .23. 如图,已知AB=DC,AC=DB.求证:∠1=∠2.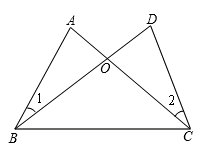 24. 如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD.
24. 如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD. (1)、求证:DB=DE;(2)、过点D作DF垂直BE,垂足为F,若CF=3,求△ABC的周长.25. 某校积极开展科技创新活动,在一次用电脑程序控制小型赛车进行50m比赛的活动中,“梦想号”和“创新号”两辆赛车在比赛前进行结对练习,两辆车从起点同时出发,“梦想号”到达终点时,“创新号”离终点还差2m.已知“梦想号”的平均速度比“创新号”的平均速度快0.1m/s.(1)、求“创新号”的平均速度;(2)、如果两车重新开始练习,“梦想号”从起点向后退2m,两车同时出发,两车能否同时到达终点?请说明理由.26. 如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC,△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)、求证:DB=DE;(2)、过点D作DF垂直BE,垂足为F,若CF=3,求△ABC的周长.25. 某校积极开展科技创新活动,在一次用电脑程序控制小型赛车进行50m比赛的活动中,“梦想号”和“创新号”两辆赛车在比赛前进行结对练习,两辆车从起点同时出发,“梦想号”到达终点时,“创新号”离终点还差2m.已知“梦想号”的平均速度比“创新号”的平均速度快0.1m/s.(1)、求“创新号”的平均速度;(2)、如果两车重新开始练习,“梦想号”从起点向后退2m,两车同时出发,两车能否同时到达终点?请说明理由.26. 如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC,△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.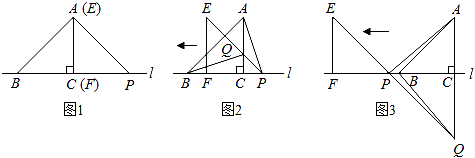 (1)、直接写出AB与AP所满足的数量关系: , AB与AP的位置关系:;(2)、将△ABC沿直线l向右平移到图2的位置时,EP交AC于点Q,连接AP,BQ,求证:AP=BQ;(3)、将△ABC沿直线l向右平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,试探究AP=BQ是否仍成立?并说明理由.
(1)、直接写出AB与AP所满足的数量关系: , AB与AP的位置关系:;(2)、将△ABC沿直线l向右平移到图2的位置时,EP交AC于点Q,连接AP,BQ,求证:AP=BQ;(3)、将△ABC沿直线l向右平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,试探究AP=BQ是否仍成立?并说明理由.