2017年人教版初中数学八年级下学期期中模拟卷
试卷更新日期:2017-04-13 类型:期中考试
一、单选题
-
1. 下列各式计算正确的是( )A、8 ﹣2 =6 B、5 +5 =10 C、4 ÷2 =2 D、4 ×2 =82. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、3. 若 =x﹣5,则x的取值范围是( )A、x<5 B、x≤5 C、x≥5 D、x>54.
如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长是( )
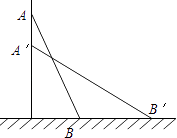
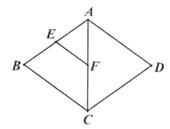 A、12 B、16 C、20 D、245. 计算×÷的结果是( )A、 B、 C、 D、6.
A、12 B、16 C、20 D、245. 计算×÷的结果是( )A、 B、 C、 D、6.如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为( )
 A、4 B、5 C、6 D、77. 已知一个平行四边形两邻边的长分别为4和7,那么它的周长为( )A、11 B、18 C、22 D、288. 将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )A、h≤17 B、h≥8 C、15≤h≤16 D、7≤h≤169. 如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为( )
A、4 B、5 C、6 D、77. 已知一个平行四边形两邻边的长分别为4和7,那么它的周长为( )A、11 B、18 C、22 D、288. 将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )A、h≤17 B、h≥8 C、15≤h≤16 D、7≤h≤169. 如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为( )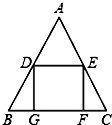 A、 cm B、4cm C、 cm D、2 cm10. 如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( )
A、 cm B、4cm C、 cm D、2 cm10. 如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( )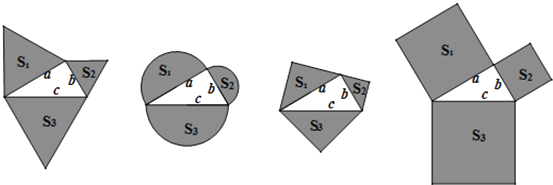 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 代数式 有意义的条件是 .12. 若实数x,y满足|x﹣3|+ =0,则( )2016的值是 .13. 已知实数x、y满足 +|y+3|=0,则x+y的值为 .14. 一艘轮船以20km/h的速度离开港口向东北方向航行,另一艘轮船同时离开港口以30km/h的速度向东南方向航行,它们离开港口半小时后相距km.15. 如图:有一个圆柱,底面圆的直径AB= ,高BC=12,P为BC的中点,蚂蚁从A点爬到P点的最短距离是 .
 16. 如图,四边形ABCD的两条对角线AC,BD互相垂直,A1 , B1 , C1 , D1是四边形ABCD的中点四边形,如果AC=8,BD=10,那么四边形A1B1C1D1的面积为 .
16. 如图,四边形ABCD的两条对角线AC,BD互相垂直,A1 , B1 , C1 , D1是四边形ABCD的中点四边形,如果AC=8,BD=10,那么四边形A1B1C1D1的面积为 .
三、计算题
-
17. 当2<m<3时,化简 ﹣3|m﹣4|.18. 已知,a= +5,b= ﹣5,求:a2+b2+5的平方根.19. 观察下列一组式的变形过程,然后回答问题:
例1: = = = = ﹣1.
例2: = ﹣ , = ﹣ , = ﹣
利用以上结论解答以下问题:
(1)、 =; =;(2)、你用含n(n为正整数)的关系式表示上述各式子的变形规律.(3)、应用上面的结论,求下列式子的值.+ + +…+
(4)、拓展提高,求下列式子的值.+ + +…+ .
四、解答题
-
20. 已知y= +9,求代数式 的值.21. 已知:如图,在矩形ABCD中,点E,F分别在AB,CD边上,BE=DF,连接CE,AF.求证:AF=CE.
 22. 如图所示,∠B=∠OAF=90°,BO=3cm,AB=4cm,AF=12cm,求图中半圆的面积.
22. 如图所示,∠B=∠OAF=90°,BO=3cm,AB=4cm,AF=12cm,求图中半圆的面积.
五、综合题