湘教版八年级数学上册 2.3.1等腰三角形的性质 同步练习
试卷更新日期：2019-01-21 类型：同步测试
一、选择题
-
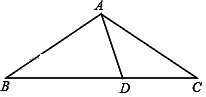
1. 如图，在△ABC中，AB=AC，∠B=40°，D为BC上一点，且AB=BD，则∠DAC的度数为（ ）
A、20° B、30° C、40° D、50°2. 如图，在 中，以点 为圆心，以 长为半径画弧交边 于点 ，连接 .若 ， ，则 的度数是（ ）
A、70° B、44° C、34° D、24°3. 如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是（ ）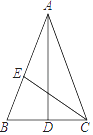
A、20° B、35° C、40° D、70°4. 如图，在Rt△ABC中，∠BAC=90°，AB=AC，点A，点C分别在直线a，b上，且a∥b．若∠1=60°，则∠2的度数为（ ）
A、105° B、75° C、135° D、155°5. 等腰三角形中有一个角是40°，则另外两个角的度数是（ ）A、70°，70° B、40°，100° C、70°，40° D、70°，70°或40°，100°二、填空题
-
6. 如图，在等边三角形ABC中，点D是边BC的中点，则∠BAD= ．
7. 在△ABC中，AB=AC，∠BAC=100°，点D在BC边上，连接AD，若△ABD为直角三角形，则∠ADC的度数为 ．8. 如图，在等腰三角形纸片ABC中，AB=AC，∠A=50°，折叠该纸片，使点A落在点B处，折痕为DE，则∠CBE= ．
9. 如图，在三角形ABC中，AD=AC=BC，∠CDA=70°，则∠DCB的度数是.
三、解答题
