湘教版八年级数学上册 2.1.2三角形的内角和与外角同步练习

试卷更新日期：2019-01-21 类型：同步测试

进入出卷网下载

一、选择题

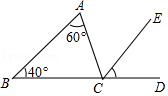
1. 直角三角形中两锐角之差为20°，则较大锐角为（）

A、45° B、55° C、65° D、50°

查看试题解析
2. 如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A=60°，∠B=40°，则∠ECD等于（）

A、40° B、45° C、50° D、55°

查看试题解析
3. 如图，AB∥CD，∠1=45°，∠3=80°，则∠2的度数为（）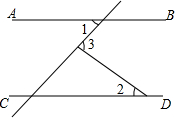

A、30° B、35° C、40° D、45°

查看试题解析
4. 如图，点D在△ABC的边AB的延长线上，DE∥BC，若∠A＝35°，∠C＝24°，则∠D的度数是（）。

A、24° B、59° C、60° D、69°

查看试题解析
5. 在下列条件中：①∠A+∠B=∠C；②∠A：∠B：∠C=1：2：3；③∠A= $\frac{1}{2}$ ∠B= $\frac{1}{3}$ ∠C；④∠A=∠B=2∠C中，能确定△ABC为直角三角形的条件有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

6. 在△ABC中，若∠A=30°，∠B=50°，则∠C= ．

查看试题解析
7. 在直角三角形中，一个锐角比另外一个锐角的 3 倍还多10°，则这两个角分别为。

查看试题解析
8. 如图，在 $Δ A B C$ 中，点 $D$ 、 $E$ 分别在 $A B$ 、 $B C$ 上，且 $D E$ // $A C$ ， $∠ A = 80^{o}$ ， $∠ B E D = 55^{o}$ ，则∠ABC=.

查看试题解析
9. 如图，在△ABC中，BD和CE是△ABC的两条高线，若∠A=65°，则∠1+∠2的度数为.

查看试题解析

三、解答题

10. 已知：如图，△ABC是任意一个三角形，求证：∠A+∠B+∠C=180°．

查看试题解析
11. △ABC中，∠C=60°，∠B的两倍比∠A大15°，求∠A和∠B的大小．

查看试题解析
12. 如图，在△ABC中，∠A＝40°，∠B＝72°，CD是AB边上的高，CE是∠ACB的平分线，DF⊥CE于F，求∠CDF的度数．

查看试题解析