2016-2017学年天津市红桥区九年级上学期期中数学试卷
试卷更新日期:2017-04-13 类型:期中考试
一、选择题
-
1. 下列方程中,关于x的一元二次方程是( )A、x2﹣2x﹣3=0 B、x2﹣2y﹣1=0 C、x2﹣x(x+3)=0 D、ax2+bx+c=02. 将一元二次方程4x2+5x=81化为一般形式后,二次项系数、一次项系数、常数项分别为( )A、4,5,81 B、4,5,﹣81 C、4,5,0 D、4x2 , 5x,﹣813. 下列图案中既是中心对称图形,又是轴对称图形的是( )A、
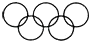 B、
B、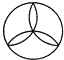 C、
C、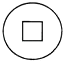 D、
D、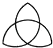 4. 关于x的一元二次方程x2﹣3x+m=0有两个不相等的实数根,则实数m的取值范围是( )A、m> B、m= C、m< D、m<﹣5. 如图,点A,B,C是⊙O上的三点,已知∠ACB=50°,那么∠AOB的度数是( )
4. 关于x的一元二次方程x2﹣3x+m=0有两个不相等的实数根,则实数m的取值范围是( )A、m> B、m= C、m< D、m<﹣5. 如图,点A,B,C是⊙O上的三点,已知∠ACB=50°,那么∠AOB的度数是( ) A、90° B、95° C、100° D、120°6. 函数y=﹣x2+1的图象大致为( )A、
A、90° B、95° C、100° D、120°6. 函数y=﹣x2+1的图象大致为( )A、 B、
B、 C、
C、 D、
D、 7. 抛物线y=﹣ x2+ x﹣1,经过配方化成y=a(x﹣h)2+k的形式是( )A、 B、 C、 D、8. 二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
7. 抛物线y=﹣ x2+ x﹣1,经过配方化成y=a(x﹣h)2+k的形式是( )A、 B、 C、 D、8. 二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:x
…
﹣5
﹣4
﹣3
﹣2
﹣1
0
…
y
…
4
0
﹣2
﹣2
0
4
…
下列说法正确的是( )
A、抛物线的开口向下 B、当x>﹣3时,y随x的增大而增大 C、二次函数的最小值是﹣2 D、抛物线的对称轴是x=﹣9. 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OA交圆O于点F,则∠CBF等于( ) A、12.5° B、15° C、20° D、22.5°10. 已知x1是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根,记△=b2﹣4ac,M=(2ax1+b)2 , 则关于△与M大小关系的下列说法中,正确的是( )A、△>M B、△=M C、△<M D、无法确定△与M的大小11. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论:
A、12.5° B、15° C、20° D、22.5°10. 已知x1是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根,记△=b2﹣4ac,M=(2ax1+b)2 , 则关于△与M大小关系的下列说法中,正确的是( )A、△>M B、△=M C、△<M D、无法确定△与M的大小11. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论:①当x=3时,y=0;
②3a+b>0;
③﹣1≤a≤﹣ ;
④ ≤n≤4.
其中正确的有( )
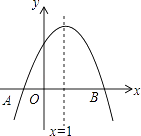 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
12. 已知方程x2+100x+10=0的两根分别为x1 , x2 , 则x1x2﹣x1﹣x2的值等于 .13. 将二次函数y=﹣x2+2x+4的图象向下平移1个单位后,所得图象对应函数的最大值为 .14. 如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于 .
 15. 某工厂实行技术改造,产量年均增长率为x,已知2009年产量为1万件,那么2011年的产量y与x间的关系式为(万件).16. 如图,直线L1∥L2 , 圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于 .
15. 某工厂实行技术改造,产量年均增长率为x,已知2009年产量为1万件,那么2011年的产量y与x间的关系式为(万件).16. 如图,直线L1∥L2 , 圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于 . 17. 如图,抛物线y=x2+bx+ 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .
17. 如图,抛物线y=x2+bx+ 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .
三、解答题
-
18. 用适当的方法解下列方程:(1)、x(x﹣1)=3﹣3x(2)、2x2﹣4x﹣1=0(配方法)19. 如图所示,BC为⊙O的直径,弦AD⊥BC于E,∠C=60°.
求证:△ABD为等边三角形.
 20. 如图,已知抛物线y=ax2+bx﹣3的对称轴为直线x=1,交x轴于A、B两点,交y轴于C点,其中B点的坐标为(3,0).
20. 如图,已知抛物线y=ax2+bx﹣3的对称轴为直线x=1,交x轴于A、B两点,交y轴于C点,其中B点的坐标为(3,0).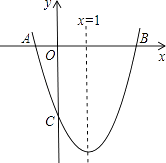 (1)、直接写出A点的坐标;(2)、求二次函数y=ax2+bx﹣3的解析式.21. 已知关于x的方程x2﹣(2k+1)x+4(k﹣ )=0(1)、求证:无论k取何值,这个方程总有实数根;(2)、若等腰三角形ABC的一边长a=4,另两边b、c恰好是这个方程的两个根,求△ABC的周长.22. 如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地.
(1)、直接写出A点的坐标;(2)、求二次函数y=ax2+bx﹣3的解析式.21. 已知关于x的方程x2﹣(2k+1)x+4(k﹣ )=0(1)、求证:无论k取何值,这个方程总有实数根;(2)、若等腰三角形ABC的一边长a=4,另两边b、c恰好是这个方程的两个根,求△ABC的周长.22. 如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地. (1)、设通道的宽度为x米,则a=(用含x的代数式表示);(2)、若塑胶运动场地总占地面积为2430平方米.请问通道的宽度为多少米?23. 如图,抛物线y= x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)、设通道的宽度为x米,则a=(用含x的代数式表示);(2)、若塑胶运动场地总占地面积为2430平方米.请问通道的宽度为多少米?23. 如图,抛物线y= x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).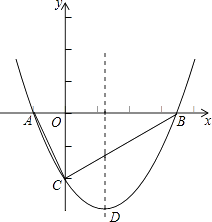 (1)、求抛物线的解析式及顶点D的坐标;(2)、判断△ABC的形状,证明你的结论;(3)、点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.24. 在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点,现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).
(1)、求抛物线的解析式及顶点D的坐标;(2)、判断△ABC的形状,证明你的结论;(3)、点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.24. 在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点,现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图). (1)、旋转过程中,当MN和AC平行时,求正方形OABC旋转的角度;(2)、试证明旋转过程中,△MNO的边MN上的高为定值;(3)、折△MBN的周长为p,在旋转过程中,p值是否发生变化?若发生变化,说明理由;若不发生变化,请给予证明,并求出p的值.
(1)、旋转过程中,当MN和AC平行时,求正方形OABC旋转的角度;(2)、试证明旋转过程中,△MNO的边MN上的高为定值;(3)、折△MBN的周长为p,在旋转过程中,p值是否发生变化?若发生变化,说明理由;若不发生变化,请给予证明,并求出p的值.