陕西省汉中市2019届高考文数二模试卷
试卷更新日期:2019-01-21 类型:高考模拟
一、单选题
-
1. 已知全集 ,集合 0,1, , ,则如图中阴影部分所表示的集合为
 A、
A、 0,
0,  B、
B、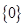 C、
C、 D、
D、 0,
0,  2. 设复数 满足 ,则 ( )A、
2. 设复数 满足 ,则 ( )A、 B、
B、 C、
C、 D、
D、 3. 已知角 的终边过点 ,则A、 B、
3. 已知角 的终边过点 ,则A、 B、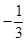 C、3
D、
4. “ ”是“ ”的A、充要条件 B、充分而不必要条件 C、必要而不充分条件 D、既不充分也不必要条件5. 某几何体的三视图如图所示,则该几何体的体积为
C、3
D、
4. “ ”是“ ”的A、充要条件 B、充分而不必要条件 C、必要而不充分条件 D、既不充分也不必要条件5. 某几何体的三视图如图所示,则该几何体的体积为 A、
A、 B、
B、 C、
C、 D、
D、 6. 设实数x,y满足 ,则 的最小值为A、
6. 设实数x,y满足 ,则 的最小值为A、 B、
C、
B、
C、 D、5
7. 已知函数 ,若 ,则实数 的值等于( )A、 B、
D、5
7. 已知函数 ,若 ,则实数 的值等于( )A、 B、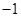 C、
C、 D、
8. 《九章算术》是我国古代的数学巨著,内容极为丰富,其中卷六《均输》里有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”意思是:“5人分取5钱,各人所得钱数依次成等差数列,其中前2人所得钱数之和与后3人所得钱数之和相等.”(“钱”是古代的一种重量单位),则其中第二人分得的钱数是( )A、 B、1 C、
D、
8. 《九章算术》是我国古代的数学巨著,内容极为丰富,其中卷六《均输》里有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”意思是:“5人分取5钱,各人所得钱数依次成等差数列,其中前2人所得钱数之和与后3人所得钱数之和相等.”(“钱”是古代的一种重量单位),则其中第二人分得的钱数是( )A、 B、1 C、 D、
9. 如图所示的程序框图,程序运行时,若输入的 ,则输出的S的值为
D、
9. 如图所示的程序框图,程序运行时,若输入的 ,则输出的S的值为 A、4 B、5 C、8 D、910. 汉中电视台“关注汉中”栏目的播出时间是每天中午12:30到13:00,在该档节目中将随机安排播出时长5分钟的有关“金色花海真美汉中”的新闻报道 若小张于某天12:50打开电视,则他能收看到这条新闻的完整报道的概率是A、
A、4 B、5 C、8 D、910. 汉中电视台“关注汉中”栏目的播出时间是每天中午12:30到13:00,在该档节目中将随机安排播出时长5分钟的有关“金色花海真美汉中”的新闻报道 若小张于某天12:50打开电视,则他能收看到这条新闻的完整报道的概率是A、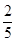 B、
C、
B、
C、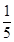 D、
D、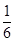 11. 设 为双曲线 : ( , )的右焦点, ,若直线 与 的一条渐近线垂直,则 的离心率为( )A、 B、
11. 设 为双曲线 : ( , )的右焦点, ,若直线 与 的一条渐近线垂直,则 的离心率为( )A、 B、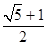 C、
C、 D、
D、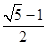 12. 若关于x的方程 存在三个不等实根,则实数a的取值范围是( )A、
12. 若关于x的方程 存在三个不等实根,则实数a的取值范围是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 已知向量 , ,若 ,则 .14. 已知正项等比数列{an}中,a1=1,其前n项和为Sn(n∈N*),且 ,则S4= .15. 已知 的内角 的对边分别为 ,且 , ,则 .16. 已知抛物线 的焦点为 是抛物线 上的两个动点,若 ,则 的最大值为 .
三、解答题
-
17. 已知函数 .(1)、求 的最小值及取得最小值时所对应的 的值;(2)、求 的单调递减区间.18. 陕西理工大学开展大学生社会实践活动,用“10分制”随机调查汉台区某社区居民的幸福指数,现从调查人群中随机抽取16人,如图所示的茎叶图记录了他们的幸福指数的得分 以小数点的前一位数字为茎,小数点后的一位数字为叶 :
 (1)、写出这组数据的众数和中位数;(2)、若幸福指数不低于9分,则称该人的幸福指数为“极幸福”;若幸福指数不高于8分,则称该人的幸福指数为“不够幸福” 现从这16人中幸福指数为“极幸福”和“不够幸福”的人中任意选取2人,求选出的两人的幸福指数均为“极幸福”的概率.19. 如图,AB为圆O的直径,点E,F在圆O上, ,矩形ABCD和圆O所在的平面互相垂直,已知 , .
(1)、写出这组数据的众数和中位数;(2)、若幸福指数不低于9分,则称该人的幸福指数为“极幸福”;若幸福指数不高于8分,则称该人的幸福指数为“不够幸福” 现从这16人中幸福指数为“极幸福”和“不够幸福”的人中任意选取2人,求选出的两人的幸福指数均为“极幸福”的概率.19. 如图,AB为圆O的直径,点E,F在圆O上, ,矩形ABCD和圆O所在的平面互相垂直,已知 , . (1)、求证:平面 平面CBF;(2)、当 时,求多面体FABCD的体积.20. 已知两定点 , ,动点 使直线 , 的斜率的乘积为 .(1)、求动点 的轨迹 的方程;(2)、过点 的直线与 交于 , 两点,是否存在常数 ,使得 ?并说明理由.
(1)、求证:平面 平面CBF;(2)、当 时,求多面体FABCD的体积.20. 已知两定点 , ,动点 使直线 , 的斜率的乘积为 .(1)、求动点 的轨迹 的方程;(2)、过点 的直线与 交于 , 两点,是否存在常数 ,使得 ?并说明理由.