2016-2017学年天津市河西区九年级上学期期中数学试卷

试卷更新日期：2017-04-13 类型：期中考试

进入出卷网下载

一、选择题

1. 下列各点，不在二次函数y=x²的图象上的是（）

A、（1，﹣1） B、（1，1） C、（﹣2，4） D、（3，9）

查看试题解析
2.
如图图案中，可以看做是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 平行四边形ABCD的四个顶点都在圆O上，那么四边形ABCD一定是（）

A、正方形 B、矩形 C、菱形 D、以上都不对

查看试题解析
4. 如图，四边形ABCD内接于圆O，若∠BOD=138°，则它的一个外角∠DCE的度数为（）

A、138° B、69° C、52° D、42°

查看试题解析
5. 在下列4个不同的情境中，两个变量所满足的函数关系属于二次函数关系的有（）
①设正方形的边长为x面积为y，则y与x有函数关系；
②x个球队参加比赛，每两个队之间比赛一场，则比赛的场次数y与x之间有函数关系；
③设正方体的棱长为x，表面积为y，则y与x有函数关系；
④若一辆汽车以120km/h的速度匀速行驶，那么汽车行驶的里程y（km）与行驶时间x（h）有函数关系．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 下列二次函数的图象中，开口最大的是（）

A、y=x² B、y=2x² C、y= $\frac{1}{100}$ x² D、y=﹣x²

查看试题解析
7. 抛物线y=x²﹣8x的顶点坐标为（）

A、（4，16） B、（﹣4，16） C、（4，﹣16） D、（﹣4，﹣16）

查看试题解析
8. 以原点为中心，把点P（1，3）顺时针旋转90°，得到的点P′的坐标为（）

A、（3，﹣1） B、（﹣3，1） C、（1，﹣3） D、（﹣1，﹣3）

查看试题解析
9. 用60m长的篱笆围成矩形场地，矩形的面积S随着矩形的一边长L的变化而变化，要使矩形的面积最大，L的长度应为（）

A、6 $\sqrt{3}$ m B、15m C、20m D、10 $\sqrt{3}$ m

查看试题解析
10. 二次函数y=ax²+bx+c（a≠0）和正比例函数y= $\frac{2}{3}$ x的图象如图所示，则方程ax²+（b﹣ $\frac{2}{3}$ ）x+c=0（a≠0）的根的情况（）

A、两根都大于0 B、两根都等于0 C、两根都小于0 D、一根大于0，一根小于0

查看试题解析
11. 如图，将边长为2的等边三角形ABC绕点C旋转120°，得到△DCE，连接BD，则BD的长为（）

A、2 B、2.5 C、3 D、2 $\sqrt{3}$

查看试题解析

二、填空题

12. 等边三角形绕它的中心至少旋转度，才能和原图形重合．

查看试题解析
13. 二次函数y=x（x﹣6）的图象的对称轴是．

查看试题解析
14. 如图，AB是圆O的直径，弧 $\hat{B C}$ =弧 $\hat{C D}$ =弧 $\hat{D E}$ ，∠COD=48°，则∠AOE的度数为．

查看试题解析
15. 如图，弦CD垂直于⊙O的直径AB，垂足为H，且CD=2 $\sqrt{2}$ ，BD= $\sqrt{3}$ ，则AB的长为．

查看试题解析
16. 如图，等腰直角△ABC中，AC=BC，∠ACB=90°，点O分斜边AB为BO：OA=1： $\sqrt{3}$ ，将△BOC绕C点顺时针方向旋转到△AQC的位置，则∠AQC= ．

查看试题解析
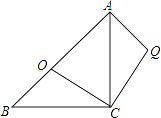17. 已知三条互相平行的直线a、b、c，请问能否作出一个等边△ABC，使其三个顶点A、B、C分别在直线a、b、c上？（用“能”或“不能”填空）．若能，请说明作图方法；若不能，请简要说明理由．

查看试题解析

三、解答题

18. 按要求画出图形：如图，△AOB是等腰直角三角形，∠AOB=90°，OA=OB，请你在图中画出以点O为中心，将△AOE逆时针旋转90°之后的图形．（不写傲法．写出结论）

查看试题解析
19. 如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径．

查看试题解析
20. 综合题。

(1)、若一抛物线的顶点在原点，且经过点A（﹣2，8），求抛物线的解析式；

(2)、如图，抛物线y=ax²+bx的顶点为A（﹣3，﹣3），且经过P（t，0）（t≠0），求该抛物线的解析式；

(3)、在（2）的条件下，回答下列问题（直接写出答案）
①y的最小值为；
②点P的坐标为；
③当x＞﹣3时，y随x的增大而．

查看试题解析
21. 如图，四边形ABCD内接于圆O，点E在对角线AC上．

(1)、若BC=DC，∠CBD=39°，求∠BCD的度数；

(2)、若在AC上有一点E，且EC=BC=DC，求证：∠1=∠2．

查看试题解析
22. 如图，点E、F、G、H分别在菱形ABCD的四条边上，且BE=BF=DG=DH，连接EF，FG，GH，HE得到四边形EFGH．

(1)、求证：四边形EFGH是矩形；

(2)、设AB=a，∠A=60°，当BE为何值时，矩形EFGH的面积最大？

查看试题解析
23. 在平面直角坐标系中，O为原点，点A（4，0），点B（0，3），把△ABO绕点B逆时针旋转，得△A′BO′，点A、O旋转后的对应点为A′、O′，记旋转角为ɑ．

(1)、
如图1，若ɑ=90°，求AA′的长；

(2)、
如图2，若ɑ=120°，求点O′的坐标．

查看试题解析
24. 如图，在平面直角坐标系中，抛物线y=﹣x²+ $\frac{1}{4}$ 与y轴相交于点A，点B与点O关于点A对称．

(1)、填空：点B的坐标为；

(2)、过点B的直线y=kx+b（其中k＜0）与x轴相交于点C，过点C作直线l平行于y轴，P是直线l上一点，且PB=PC，求线段PB的长（用含k的式子表示），并判断点P是否在抛物线上，说明理由．

查看试题解析