2016-2017学年山东省临沂市罗庄区九年级上学期期中数学试卷
试卷更新日期：2017-04-13 类型：期中考试
一、选择题
-
1. 下列关于x的方程中，是一元二次方程的是（ ）A、y2+x=1 B、x（x﹣1）=x2﹣2 C、x2﹣1=0 D、x2+ =12. 下列图案中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
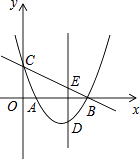
3. 若关于x的一元二次方程x2﹣mx﹣2=0的一个根为﹣1，则另一个根为（ ）A、1 B、﹣1 C、2 D、﹣24. 如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=55°，则∠BCD的度数为（ ）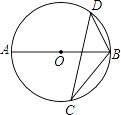
A、35° B、45° C、55° D、75°5. 抛物线y=x2+4x+1可以由抛物线y=x2平移得到，则下列平移过程正确的是（ ）A、先向左平移2个单位，再向上平移3个单位 B、先向左平移2个单位，再向下平移3个单位 C、先向右平移2个单位，再向下平移3个单位 D、先向右平移2个单位，再向上平移3个单位6. 已知三角形的两边长分别为2和4，第三边的长是方程x2﹣4x+3=0的解，则这个三角形的周长为（ ）A、3 B、9 C、7或9 D、77. 已知点P关于x轴的对称点P1的坐标是（2，3），那么点P关于原点的对称点P2的坐标是（ ）A、（﹣3，﹣2） B、（2，﹣3） C、（﹣2，﹣3） D、（﹣2，3）8. 已知关于x的一元二次方程（a﹣1）x2﹣2x+1=0有两个不相等的实数根，则a的取值范围是（ ）A、a＜2 B、a＞2 C、a＜2且a≠1 D、a＜﹣29. 设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y=﹣（x+1）2+m上的三点，则（ ）A、y1＞y2＞y3 B、y1＞y3＞y2 C、y3＞y2＞y1 D、y2＞y1＞y310. 体育局要组织一次篮球赛，赛制为单循环形式（每两队之间都赛一场），计划安排28场比赛，设应邀请x队参加比赛，则可列方程为（ ）A、x（x+1）=28 B、x（x﹣1）=28 C、x（x+1）=28 D、x（x﹣1）=2811. 已知函数y=（k﹣3）x2+2x+1的图象与x轴有交点，则k的取值范围是（ ）A、k＜4 B、k≤4 C、k＜4且k≠3 D、k≤4且k≠312. 如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（ ）
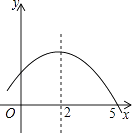A、﹣1＜x＜5 B、x＞5 C、x＜﹣1且x＞5 D、x＜﹣1或x＞513. 如图，点O是△ABC的内切圆的圆心，若∠BAC=80°，则∠BOC=（ ）
A、130° B、100° C、50° D、65°14. 如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下四个结论：①abc=0；②a+b+c＞0；③a＞b；④b2﹣4ac＜0；其中正确的结论有（ ）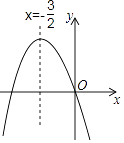
A、1个 B、2个 C、3个 D、4个二、填空题
-
15. 已知代数式的值x2+3x+5的值为7，则代数式3x2+9x﹣1的值为 ．16. 如图，AB是⊙O的弦，AB长为8，P是⊙O上一个动点（不与A、B重合），过点O作OC⊥AP于点C，OD⊥PB于点D，则CD的长为 ．
17. 某一型号飞机着陆后滑行的距离y（单位：m）与滑行时间x（单位：s）之间的函数关系式是y=60x﹣1.5x2 ， 该型号飞机着陆后滑行m才能停下来．18.如图，△COD是△AOB绕点O顺时针旋转40°后得到的图形，若点C恰好落在AB上，且∠AOD的度数为90°，则∠B的度数是 ．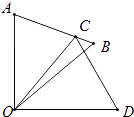
19. 如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则EC的长为 ．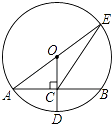
三、解答题
-
20. 解方程(1)、x2﹣4x﹣32=0(2)、3x（x+3）=x2﹣9．21.
如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．
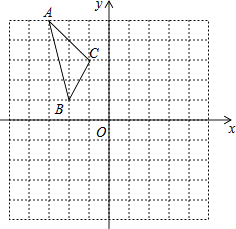(1)、若△ABC经过平移后得到△A1B1C1 ， 已知点C1的坐标为（4，0），写出顶点A1 ， B1的坐标；(2)、若△ABC和△A2B2C2关于原点O成中心对称图形，写出△A2B2C2的各顶点的坐标；(3)、将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 ， 写出△A3B3C3的各顶点的坐标．22. 某地2014年为做好“精准扶贫”，投入资金1280万元用于异地安置，并规划投入资金逐年增加，2016年在2014年的基础上增加投入资金1600万元．(1)、从2014年到2016年，该地投入异地安置资金的年平均增长率为多少？(2)、在2016年异地安置的具体实施中，该地计划投入资金不低于500万元用于优先搬迁租房奖励，规定前1000户（含第1000户）每户每天奖励8元，1000户以后每户每天补助5元，按租房400天计算，试求今年该地至少有多少户享受到优先搬迁租房奖励？23. 一个边长为4的等边三角形ABC与⊙O等高，如图放置，⊙O与BC相切于点C，⊙O与AC相交于点E．
(1)、求CE的长；(2)、求阴影部分的面积．
