2016-2017学年山东省济宁市微山县九年级上学期期中数学试卷
试卷更新日期：2017-04-13 类型：期中考试
一、选择题
-
1. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列方程是关于X的一元二次方程的是（ ）A、2x2+3=x（2x一1） B、 C、x2=0 D、ax2+bx+c=03. 若关于x的一元二次方程x2+bx+c=0的两个实数根分别为x1=﹣2，x2=4，则b+c的值是（ ）A、﹣10 B、10 C、﹣6 D、﹣14. 下列事件属于必然事件的是（ ）A、明天太阳从东方升起 B、购买2张彩票，其中1张中奖 C、随机掷一枚骰子，朝上一面上的数字大于6 D、投篮10次，一次都没投中5. 如图，PA与⊙O相切于点A，PO交⊙O于点C，点B是优弧CBA上一点，若∠P=26°，则∠ABC的度数为（ ）
A、26° B、64° C、32° D、90°6. 如图，从一块直径是2的圆形硬纸片上剪出一个圆心角为90°扇形．则这个扇形的面积为（ ）
A、π B、 π C、 π D、 π7. 如图，抛物线y=﹣x2﹣2x+3与x轴交于点A，B，把抛物线与线段AB围成的图形记为C1 ， 将Cl绕点B中心对称变换得C2 ， C2与x轴交于另一点C，将C2绕点C中心对称变换得C3 ， 连接C，与C3的顶点，则图中阴影部分的面积为（ ）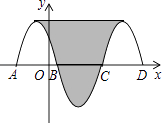
A、32 B、24 C、36 D、488. 如图，AB是⊙D的直径，AD切⊙D于点A，EC=CB．则下列结论：①BA⊥DA；②OC∥AE；③∠COE=2∠CAE；④OD⊥AC．一定正确的个数有（ ）
A、4个 B、3个 C、2个 D、1个9. 如图，抛物线y=ax2+bx+c （a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（-1，0），其部分图象如图所示，下列结论：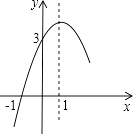
①4ac＜b2；
②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；
③3a+c＞0；
④当y＞0时，x的取值范围是﹣1≤x＜3；
⑤若（﹣ ，y1），（ ，y2）是抛物线上两点，则y1＜y2 ．其中结论正确的个数是（ ）
A、4个 B、3个 C、2个 D、1个二、填空题
-
10. 关于x的一元二次方程群ax2+bx+1=0有两个相等的实数根，写出一组满足条件的实数a，b的值 ．11. 把抛物线y=x2+bx+c向右平移3个单位长度，再向上平移2个单位长度，所得函数图象的解析式是y=x2﹣2x+5，则b+c= ．12. 在1×3的正方形网格格点上放三枚棋子，按图所示的位置己放置了两枚棋子，若第三枚棋子随机放在其他格点上，则以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为 ．
13. 二次函数y=ax2+bx+c （a≠0）（a≠0，a，b，C为常数）的图象，若关于x的一元二次方程ax2+bx+c=m有实数根，则m的取值范围是 ．
14. 如图所示，⊙D内切△ABC，切点分别为M，G，N，DE切0D于F点，交AC，AB于点D，E，若△ABC的周长为l2，BC=2，则△ADE的周长是 ．
三、解答题
-
15. 解方程：3x（x﹣2）=2（2﹣x）；16. 如图，点D在等边△ABC的边BC上．
(1)、把△ACD绕点A顺时针旋转，使点C与点B重合，画出旋转后的△ABD′；(2)、如果AC=4，CD=1，求（1）中点D旋转所走过的路程．17. 一天，小明和小智一起玩卡片游戏，他们分别握有三张正面分别标有字母A，B，C，的不透明卡片．游戏约定：每人将各自的卡片背面朝工弄洗均匀，然后随机抽取一张，两张卡片中，如果同为元音或辅音字母，则为平局；如果一个元音字母一个辅音字母，则抽到元音字母者获胜．(1)、请用列表或画树状图的方法列举出所有出现结果的可能性；(2)、求小明获胜的概率．18. 2016年9月5日，二十国集团领导人杭州峰会在杭州国际博览中心继续举行，这次峰会吸引了大批游客在“十一”假期间前往杭州旅游．为抓住商机，两个商家对同样一件售价为50元/个的产品进行促销活动．甲商家用如下方法促销：若购买该商品不超过10个，按原价付款：若一次购买10个以上．且购买的个数每增加一个，其价格减少l元，但该商品的售价不得低于35元/个；乙店一律按原价的80%销售．现购买该商品x个，如果全部在甲商家购买，则所需金额为y1元：如果全部在乙商家购买，则所需金额为y2元．(1)、分别求出y1 ， y2与x之间的函数关系式；(2)、若一位游客花800元，最多能购买多少个该商品？19. 已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．(1)、如图①，当直线l与⊙O相切于点C时，求证：AC平分∠DAB；
(2)、如图②，当直线l与⊙O相交于点E，F时，求证：∠DAE=∠BAF．
20. 阅读下面材料【材料一】按一定顺序排列的一列数称为数列，记作：{an}（n属于正整数）．数列中的每一个数都叫做这个数列的项，排在第一位的数称为这个数列的第1项
（通常也叫做首项），记作：a1；排在第二位的数称为这个数列的第2项，记作：a2；…；排在第打位的数称为这个数列的第n项，记作：an ．
【材料二】如果一个数列从第二项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列．这个常数叫做等差数列的公差，公差常用字母d表示．
例如：数列10，15，20，25是等差数列．
如果数列a1 ， a2 ， a3 ， …，an ， …是等差数列，那么a2﹣a1=d，a3﹣a2=d，…，
an﹣an﹣1=d．即：a2=a1+d，a3=a2+d=al+d+d=a1+2d，a4=a3+d=a1+3d，…．
根据上述材料，解答问题
(1)、下列数列属于等差数列的是 （只填序号）．①1，2，3，4，5．②2，4，6，8，10，11．③1，1，1，1，1．
(2)、已知数列{an}是等差数列，①a1=1，a2=4，a3=7，…．则a10= ．
②首项a1=23，公差d=2，则an= ．
(3)、已知等差数列{an}满足a2=0，a6+a8=﹣10．求an ．21.在Rt△OAB中，∠AOB=90°，已知AB= ，AO：BO=1：3，将△OAB绕点O按顺时针方向旋转90°得到△ODC，如图1建立平面直角坐标系．
(1)、求A，B，C三点坐标；(2)、若抛物线y=ax2+bx+c（a≠0）经过A，B，C三点（如图2），点P是抛物线的顶点，试判定△PCD的形状，并说明理由：
(3)、在（2）的抛物线上，且在第一象限中，是否存在点Q，使S△QCD=S△OCD？若存在，请求点Q的横坐标；若不存在，请说明理由．