2016-2017学年山东省东营市垦利县九年级上学期期中数学试卷（五四制）

试卷更新日期：2017-04-13 类型：期中考试

进入出卷网下载

一、选择题

1. 一元二次方程（x+6）²﹣9=0的解是（）

A、x₁=6，x₂=﹣6 B、x₁=x₂=﹣6 C、x₁=﹣3，x₂=﹣9 D、x₁=3，x₂=﹣9

查看试题解析
2. 下列所述图形中，是中心对称图形的是（）

A、直角三角形 B、平行四边形 C、正五边形 D、正三角形

查看试题解析
3. 如图，在半径为5cm的⊙O中，弦AB=6cm，OC⊥AB于点C，则OC=（）

A、3cm B、4cm C、5cm D、6cm

查看试题解析
4. 将抛物线y=x²﹣4x﹣4向左平移3个单位，再向上平移5个单位，得到抛物线的函数表达式为（）

A、y=（x+1）²﹣13 B、y=（x﹣5）²﹣3 C、y=（x﹣5）²﹣13 D、y=（x+1）²﹣3

查看试题解析
5. 关于x的一元二次方程x²+ax﹣1=0的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
6. 在平面直角坐标系中，将△AOB绕原点O顺时针旋转180°后得到△A₁OB₁ ，若点B的坐标为（2，1），则点B的对应点B₁的坐标为（）

A、（﹣2，﹣1） B、（2，﹣1） C、（﹣2，1） D、（1，2）

查看试题解析
7. 有x支球队参加篮球比赛，共比赛了45场，每两队之间都比赛一场，则下列方程中符合题意的是（）

A、 $\frac{1}{2}$ x（x﹣1）=45 B、 $\frac{1}{2}$ x（x+1）=45 C、x（x﹣1）=45 D、x（x+1）=45

查看试题解析
8. 抛物线y=2x²﹣2 $\sqrt{2}$ x+1与坐标轴的交点个数是（）

A、0 B、1 C、2 D、3

查看试题解析
9. 如图，从一张腰长为60cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的高为（）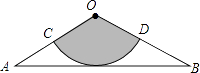

A、10cm B、15cm C、10 $\sqrt{3}$ cm D、20 $\sqrt{2}$ cm

查看试题解析
10. 已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，并且关于x的一元二次方程ax²+bx+c﹣m=0有两个不相等的实数根，下列结论：
①b²﹣4ac＜0；②abc＞0；③a﹣b+c＜0；④m＞﹣2，
其中，正确的个数有（）

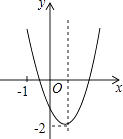A、1 B、2 C、3 D、4

查看试题解析

二、填空题

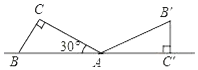
11. 方程x²﹣5x=0的解是．

查看试题解析
12. 如图所示，将一个含30°角的直角三角板ABC绕点A旋转，使得点B，A，C′在同一条直线上，则三角板ABC旋转的角度是．

查看试题解析
13. 如图，∠A是⊙O的圆周角，∠OBC=55°，则∠A= ．

查看试题解析
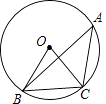14. 抛物线y=x²﹣2x+1的顶点坐标是．

查看试题解析
15. 关于x的一元二次方程2x²+3x﹣m=0有两个不相等的实数根，则m的取值范围是．

查看试题解析
16. 如图，抛物线y=﹣x²+2x+3与y轴交于点C，点D（0，1），点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为．

查看试题解析
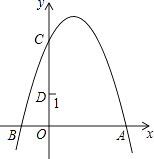17. 如图，C为半圆内一点，O为圆心，直径AB长为2cm，∠BOC=60°，∠BCO=90°，将△BOC绕圆心O逆时针旋转至△B′OC′，点C′在OA上，则边BC扫过区域（图中阴影部分）的面积为cm² ．

查看试题解析
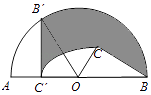18. 如图，将一张等边三角形纸片沿中位线剪成4个小三角形，称为第一次操作；然后，将其中的一个三角形按同样方式再剪成4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得到10个小三角形，称为第三次操作；…根据以上操作，若要得到100个小三角形，则需要操作的次数是．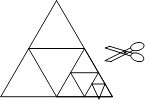

查看试题解析

三、解答题

19. 计算：﹣2⁴﹣ $\sqrt{12}$ +|1﹣2 $\sqrt{3}$ |+（ $\frac{1}{2016}$ ）^﹣¹+（π﹣ $\frac{2}{3}$ ）⁰ ．

查看试题解析
20. 先化简，再求值： $\frac{a^{2} + a}{a^{2} - 2 a + 1}$ $\div (\frac{2}{a - 1} - \frac{1}{a})$ ，其中a是方程2x²+x﹣3=0的解．

查看试题解析
21.
如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．

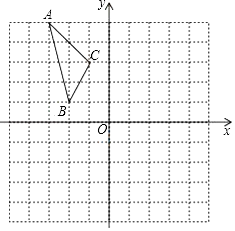(1)、若△ABC经过平移后得到△A₁B₁C₁ ，已知点C₁的坐标为（4，0），写出顶点A₁ ， B₁的坐标，并画出△A₁B₁C₁；

(2)、若△ABC和△A₂B₂C₂关于原点O成中心对称图形，写出△A₂B₂C₂的各顶点的坐标；

(3)、将△ABC绕着点O按顺时针方向旋转90°得到△A₃B₃C₃ ，写出△A₃B₃C₃的各顶点的坐标，并画出△A₃B₃C₃ ．

查看试题解析
22. 如图，△ABC中，AB=AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F．

(1)、试说明DF是⊙O的切线；

(2)、若AC=3AE，求 $\frac{B E}{C E}$ 的值．

查看试题解析
23. 现代互联网技术的广泛应用，催生了快递行业的高度发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同．

(1)、求该快递公司投递总件数的月平均增长率；

(2)、如果平均每人每月最多可投递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？

查看试题解析
24.
在平面直角坐标系中，平行四边形ABOC如图放置，点A、C的坐标分别是（0，4）、（﹣1，0），将此平行四边形绕点O顺时针旋转90°，得到平行四边形A′B′OC′．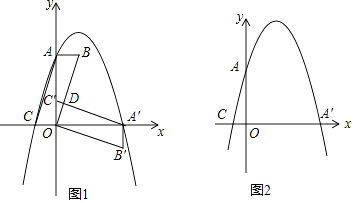

(1)、若抛物线经过点C、A、A′，求此抛物线的解析式；

(2)、点M时第一象限内抛物线上的一动点，问：当点M在何处时，△AMA′的面积最大？最大面积是多少？并求出此时M的坐标；

(3)、若P为抛物线上一动点，N为x轴上的一动点，点Q坐标为（1，0），当P、N、B、Q构成平行四边形时，求点P的坐标，当这个平行四边形为矩形时，求点N的坐标．

查看试题解析