2016-2017学年山东省德州市庆云县九年级上学期期中数学试卷

试卷更新日期：2017-04-13 类型：期中考试

进入出卷网下载

一、选择题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列函数解析式中，一定为二次函数的是（　　）

A、y=3x﹣1 B、y=ax²+bx+c C、s=2t²﹣2t+1 D、y=x²+ $\frac{1}{x}$

查看试题解析
3. 一元二次方程2x²﹣3x+1=0化为（x+a）²=b的形式，正确的是（）

A、 ${(x - \frac{3}{2})}^{2} = 16$ B、 $2 {(x - \frac{3}{4})}^{2} = \frac{1}{16}$ C、 ${(x - \frac{3}{4})}^{2} = \frac{1}{16}$ D、以上都不对

查看试题解析
4. 已知关于x的一元二次方程（k﹣2）²x²+（2k+1）x+1=0有两个不相等的实数根，则k的取值范围是（）

A、k＞ $\frac{4}{3}$ 且k≠2 B、k≥ $\frac{4}{3}$ 且k≠2 C、k＞ $\frac{3}{4}$ 且k≠2 D、k≥ $\frac{3}{4}$ 且k≠2

查看试题解析
5. 如图，将⊙O沿弦AB折叠，圆弧恰好经过圆心O，点P是优弧 $\hat{A M B}$ 上一点，则∠APB的度数为（）

A、45° B、30° C、75° D、60°

查看试题解析
6. 某航空公司有若干个飞机场，每两个飞机场之间都开辟一条航线，一共开辟了15条航线，则这个航空公司共有飞机场（）

A、5个 B、6个 C、7个 D、8个

查看试题解析
7. 将抛物线y=x²﹣2x+3向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为（）

A、y=（x﹣1）²+4 B、y=（x﹣4）²+4 C、y=（x+2）²+6 D、y=（x﹣4）²+6

查看试题解析
8. 在二次函数y=x²﹣2x﹣3中，当0≤x≤3时，y的最大值和最小值分别是（）

A、0，﹣4 B、0，﹣3 C、﹣3，﹣4 D、0，0

查看试题解析
9. 在同一坐标系中，一次函数y=ax+2与二次函数y=x²+a的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y=kx+4 $\sqrt{3}$ 与x轴、y轴分别交于A，B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（）

A、6 B、8 C、10 D、12

查看试题解析
11. 如图，已知在⊙O中，AB是弦，半径OC⊥AB，垂足为点D，要使四边形OACB为菱形，还需要添加一个条件，这个条件可以是（）

A、AD=BD B、OD=CD C、∠CAD=∠CBD D、∠OCA=∠OCB

查看试题解析
12. 如图是二次函数y=ax²+bx+c（a≠0）图象的一部分，对称轴为x= $\frac{1}{2}$ ，且经过点（2，0），有下列说法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（0，y₁），（1，y₂）是抛物线上的两点，则y₁=y₂ ．上述说法正确的是（）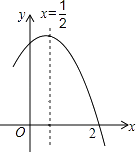

A、①②④ B、③④ C、①③④ D、①②

查看试题解析

二、填空题

13. 实数a，b是关于x的方程2x²+3x+1=0的两根，则点P（a，b）关于原点对称的点Q的坐标为．

查看试题解析
14. 某商场第一季度的利润是82.75万，其中一月份的利润是25万，若利润的平均月增长率为x，可列出方程为：．

查看试题解析
15. 已知点A（4，y₁），B（ $\sqrt{2}$ ，y₂），C（﹣2，y₃）都在二次函数y=（x﹣2）²﹣m的图象上，则y₁ ， y₂ ， y₃的大小关系为．

查看试题解析
16. 已知实数m，n满足3m²+6m﹣5=0，3n²+6n﹣5=0，且m≠n，则 $\frac{n}{m} + \frac{m}{n}$ = ．

查看试题解析
17. 如图，在Rt△ABC中，∠ACB=90°，AC=5cm，BC=12cm，将△ABC绕点B顺时针旋转60°，得到△BDE，连接DC交AB于点F，则△ACF与△BDF的周长之和为cm．

查看试题解析

三、解答题

18. 用适当的方法解下面的方程
①3x²+x﹣1=0
②（3x﹣2）²=4（3﹣x）² ．

查看试题解析
19.
如图，△ABC三个顶点的坐标分别为A（2，4），B（1，1），C（4，3）．

(1)、请画出△ABC关于原点对称的△A₁B₁C₁ ，并写出A₁的坐标；

(2)、请画出△ABC绕点B逆时针旋转90°后的△A₂B₂C₂ ．

查看试题解析
20. 某花店将进货价为20元/盒的百合花，在市场参考价28～38元的范围内定价36元/盒销售，这样平均每天可售出40盒，经过市场调查发现，在进货价不变的情况下，若每盒下调1元，则平均每天可多销售10盒，要使每天的利润达到750元，应将每盒百合花在售价上下调多少元？

查看试题解析
21. 如图，点D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．

(1)、判断直线CD和⊙O的位置关系，并说明理由．

(2)、过点B作⊙O的切线BE交直线CD于点E，若AC=2，⊙O的半径是3，求BE的长．

查看试题解析
22. 九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：
售价（元/件）
100
110
120
130
…
月销量（件）
200
180
160
140
…
已知该运动服的进价为每件60元，设售价为x元．

(1)、请用含x的式子表示：①销售该运动服每件的利润是（）元；②月销量是（）件；（直接写出结果）

(2)、设销售该运动服的月利润为y元，那么售价为多少时，当月的利润最大，最大利润是多少？

查看试题解析
23. 探究：如图1和2，四边形ABCD中，已知AB=AD，∠BAD=90°，点E、F分别在BC、CD上，∠EAF=45°．

(1)、
①如图1，若∠B、∠ADC都是直角，把△ABE绕点A逆时针旋转90°至△ADG，使AB与AD重合，则能证得
EF=BE+DF，请写出推理过程；
②如图2，若∠B、∠D都不是直角，则当∠B与∠D满足数量关系时，仍有EF=BE+DF；

(2)、
拓展：如图3，在△ABC中，∠BAC=90°，AB=AC=2 $\sqrt{2}$ ，点D、E均在边BC上，且∠DAE=45°．若BD=1，求DE的长．

查看试题解析
24.
如图，在直角坐标系中，点A的坐标为（﹣2，0），OB=OA，且∠AOB=120°．

(1)、求经过A，O，B三点的抛物线的解析式．

(2)、在（1）中抛物线的对称轴上是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由．

(3)、若点M为抛物线上一点，点N为对称轴上一点，是否存在点M，N使得A，O，M，N构成的四边形是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．

查看试题解析

售价（元/件）	100	110	120	130	…
月销量（件）	200	180	160	140	…